等差数列の一般項

数列の表記と一般項

数列 … 数を一列に並べたもの

$1，4，9，16，25，\cdots\cdots$

$1，4，7，10，13，\cdots\cdots$

$2，6，18，54，162，\cdots\cdots$

$1，2，4，7，11，\cdots\cdots$

項 … 数列における各数

数列の項は最初の項から順に第１項，第２項，第３項，……，第 $n$ 項

第１項のことを　初項　という

数列を一般的に表すために次のように書く

$a_1，a_2，a_3，\cdots\cdots，a_n$

つまり

$a_○$ が第○項

この数列を ${a_n}$ と略記することもある

第 $n$ 項の $a_n$ を数列 $\{a_n\}$ の　一般項　という

　

例　$a_n=3n-1$ である数列 $\{a_n\}$ の第 $5$ 項を求めよ。

$a_5=3\cdot5-1=14$

等差数列とは

等差数列 … 初項に一定の数を足して得られる数列

足していく一定の数のことを　公差　といい，$d$ で表す

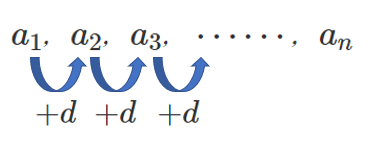
等差数列の例

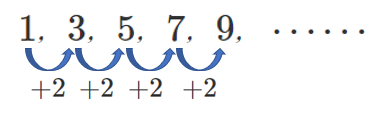
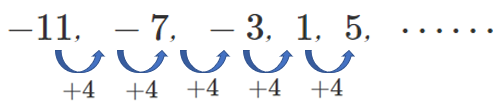
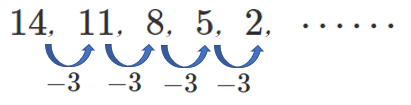
等差数列の一般項

初項 $a$，公差 $d$ の等差数列 $\{a_n\}$

\begin{eqnarray} a_1 &=& a \\ a_2 &=& a+d \\ a_3 &=& a+2d \\ a_4 &=& a+3d \\ &&\cdots\cdots \\ &&\cdots\cdots \\ &&\cdots\cdots \\ a_n &=& a+(n-1)d \\ \end{eqnarray}

　

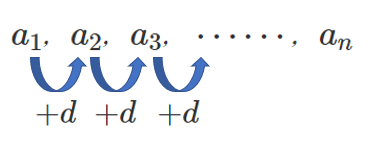
第 $2$ 項は初項に公差を $1$ 回足すと求まる

第 $3$ 項は初項に公差を $2$ 回足すと求まる

第 $4$ 項は初項に公差を $3$ 回足すと求まる

これより

第 $n$ 項は 初項に公差を $(n-1)$ 回足すと求まる

　

$a_n=2+(n-1)\cdot3=3n-1$

　

問題

初項 $a$，公差 $d$ とすると

$a_n=a+(n-1)d$

$a_3=5$ より

$a+2d=5$　$\cdots\cdots$　①

$a_6=-4$ より

$a+5d=-4$　$\cdots\cdots$　②

①，②を解くと

$a=11$，$d=-3$

したがって

$a_n=11+(n-1)\cdot(-3)=-3n+14$

　

(1)　$99$ は第何項か。

　数列 $\{a_n\}$ の一般項は

$a_n=3+(n-1)\cdot4=4n-1$

　$4n-1=99$ を解くと

$n=25$

　したがって，$99$ は　第 $25$ 項

　

(2)　初めて $300$ を超えるのは第何項か。

　$4n-1>300$ より

$\displaystyle{n>\frac{301}{4}=75.2\cdots}$

　これを満たす最小の自然数 $n$ は

$n=76$

　したがって， 初めて $300$ を超えるのは　第 $76$ 項

　

まとめ

● 等差数列の一般項

　初項 $a$，公差 $d$ の等差数列 $\{a_n\}$ の一般項は

$a_n=a+(n-1)d$