素数
素数は
$2,3,5,7,11,13,17,19,23,\cdots$

$1$ は素数でないことは覚えておこう!
合成数
合成数は
$4,6,8,9,10,12,14,15,16,\cdots$
$4=2・2$
$6=2・3$
$8=2・2・2$
$10=2・5$
$12=3・4$
以上のように合成数は $1$ 以外の整数の積で表すことができる
因数と素因数
$12=3・4$ における
$3$ と $4$ のような積を作る一つ一つを $12$ の因数という
因数の中でも素数である因数を素因数という
素因数分解とは
素因数分解とは
$60=2^2・3・5$
$126=2・3^2・7$
のように素数だけの積で表すこと
素因数分解のやり方
$60$ の素因数分解

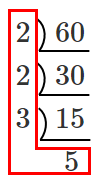
$60=2^2・3・5$
素因数分解を用いる問題
$\sqrt{60n}$ が自然数になるのは,
$60n$ がある自然数の $2$ 乗になるとき
$60=2^2・3・5$ なので
$60n=2^2・3・5・n$
$n=3・5$ のとき
$60n=(2^2・3・5)・(3・5)=2^2・3^2・5^2=(2・3・5)^2$
よって,求める最小の自然数は $n=15$

$n=15$ のとき,$\sqrt{60n}=\sqrt{900}=30$
で自然数になるね!
$\displaystyle{\sqrt{\frac{60}{n}}}$ が自然数になるのは
$\displaystyle{\frac{60}{n}}$ がある自然数の $2$ 乗になるとき
$60=2^2・3・5$ なので
$\displaystyle{\frac{60}{n}=\frac{2^2・3・5}{n}}$
$n=3・5$ のとき
$\displaystyle{\frac{60}{n}=\frac{2^2・3・5}{3・5}=2^2}$
$n=2^2・3・5$ のとき
$\displaystyle{\frac{60}{n}=\frac{2^2・3・5}{2^2・3・5}=1^2}$
よって,求める自然数は $n=15,60$

$n=15$ のとき,$\displaystyle{\sqrt{\frac{60}{n}}=\sqrt{\frac{60}{15}}=\sqrt{4}=2}$
$n=60$ のとき,$\displaystyle{\sqrt{\frac{60}{n}}=\sqrt{\frac{60}{60}}=\sqrt{1}=1}$
で自然数になるね!

$\sqrt{ }$ の中を $2$ 乗にすると $\sqrt{ }$ がとれるね!
平方根 $\sqrt{ }$ の復習はこれ↓

まとめ
● 素因数分解
素数の積の形にすること
● $\sqrt{○n}$ を自然数にする
素因数分解を用いて,$\sqrt{ }$ の中の $○n$ を $2$ 乗の形にする
問題
$\sqrt{120n}$ が自然数になるのは,
$120n$ がある自然数の $2$ 乗になるとき
$120=2^3・3・5$ なので
$120n=2^3・3・5・n$
$n=2・3・5$ のとき
$60n=(2^3・3・5)・(2・3・5)=2^4・3^2・5^2=(2^2・3・5)^2$
よって,求める最小の自然数は $n=30$

$n=30$ のとき,$\sqrt{120n}=\sqrt{3600}=60$
で自然数になるね!
$\displaystyle{\sqrt{\frac{180}{n}}}$ が自然数になるのは
$\displaystyle{\frac{180}{n}}$ がある自然数の $2$ 乗になるとき
$180=2^2・3^2・5$ なので
$\displaystyle{\frac{180}{n}=\frac{2^2・3^2・5}{n}}$
$n=5$ のとき
$\displaystyle{\frac{180}{n}=\frac{2^2・3^2・5}{5}=2^2・3^2}$
$n=2^2・5$ のとき
$\displaystyle{\frac{180}{n}=\frac{2^2・3^2・5}{2^2・5}=3^2}$
$n=3^2・5$ のとき
$\displaystyle{\frac{180}{n}=\frac{2^2・3^2・5}{3^2・5}=2^2}$
$n=2^2・3^2・5$ のとき
$\displaystyle{\frac{180}{n}=\frac{2^2・3^2・5}{2^2・3^2・5}=1^2}$
よって,求める自然数は $n=5,20,45,180$

$n=5$ のとき,
$\displaystyle{\sqrt{\frac{180}{n}}=\sqrt{\frac{180}{5}}=\sqrt{36}=6}$
$n=20$ のとき,
$\displaystyle{\sqrt{\frac{180}{n}}=\sqrt{\frac{180}{20}}=\sqrt{9}=3}$
$n=45$ のとき,
$\displaystyle{\sqrt{\frac{180}{n}}=\sqrt{\frac{180}{45}}=\sqrt{4}=2}$
$n=180$ のとき,$\displaystyle{\sqrt{\frac{180}{n}}=\sqrt{\frac{180}{180}}=\sqrt{1}=1}$
で自然数になるね!

素因数分解することで,$2$ 乗ができたかどうかが見やすいね!




コメント