組合せとは

まずは順列との違いをはっきりさせよう!
順列の復習はこれ↓

順列 … 異なる $n$ 個から異なる $r$ 個を選んで並べる
組合せ … 異なる $n$ 個から異なる $r$ 個を選ぶ
「選ぶだけ」が組合せ
組合せの具体例
$\{a,b,c\}$,$\{a,b,d\}$,$\{a,c,d\}$,$\{b,c,d\}$
の4通り
$\{a,b,c\}$,$\{a,c,b\}$,$\{b,a,c\}$
$\{b,c,a\}$,$\{c,a,b\}$,$\{c,b,a\}$
は並び順が違うので,順列では6通りだが
組合せはすべて同じなので,
組合せでは $\{a,b,c\}$ の1通りと考える

「順列は選んで並べる」
「組合せは選ぶだけ」
並べない分,組合せの方が場合の数が小さいね!
組合せの総数
異なる $n$ 個から異なる $r$ 個を選ぶ組合せを
$n$ 個から $r$ 個選ぶ組合せ という
その総数を $_nC_r$ で表す
$_nC_r$ の計算

$_nC_r$ は,順列 $_nP_r$ と $r!$ を使って表すことができるよ!
$_nP_r$ … 異なる $n$ 個から異なる $r$ 個を選んで並べる
$r!$ … 異なる $r$ 個をすべて並べる
$_nC_r$ … 異なる $n$ 個から異なる $r$ 個を選ぶ
これらを使って式を作る
$_nP_r=_nC_r×r!$
($n$ 個から $r$ 個選んで並べる)=($n$ 個から $r$ 個選ぶ)×(選んだ $r$ 個をすべて並べる)
これを式変形すると
$\displaystyle{_nC_r=\frac{_nP_r}{r!}}$

この式を使って問題を解いてみよう!
$\displaystyle{_4C_3=\frac{_4P_3}{3!}}$ より
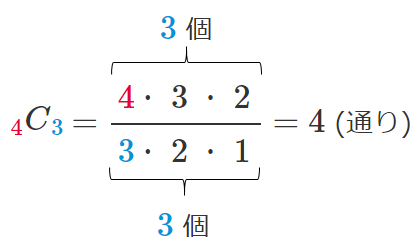

$\displaystyle{_nC_r=\frac{_nP_r}{r!}}$ を覚えるよりは下のように覚えよう!
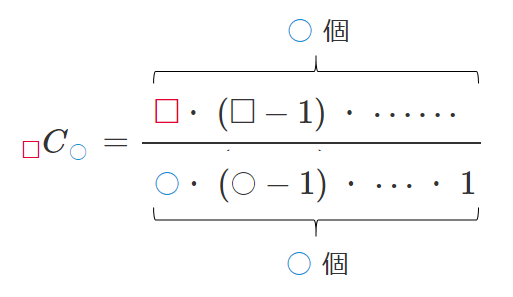
$_nC_r$ の性質

$100$ 個から $99$ 個選ぶのは何通り?

$_{100}C_{99}$ で計算できるけど,計算が大変だよ…

$100$ 個から $99$ 個選んでって言われたらどうする?

$99$ 個選ぶのは大変だから,
選ばない $1$ 個を選ぶかな?

それが効率のよい考え方だよね!
「$100$ 個から $99$ 個選ぶ」のも,
「$100$ 個から $1$ 個選ぶ」のも同じということだよ!

なるほど!
$_{100}C_{99}$ は $_{100}C_1$ で計算できるってことか!
具体例
$_6C_4=_6C_2$
$_7C_5=_7C_2$
$_8C_5=_8C_3$
$_9C_8=_9C_1$

$_nC_r$ の計算が複雑な場合は使えるようにしよう!
まとめ
● 順列と組合せの違い
「選んで並べる」が順列
「選ぶだけ」が組合せ
● 組合せ
異なる $n$ 個から異なる $r$ 個を選ぶ組合せを
$n$ 個から $r$ 個選ぶ組合せ という
その総数を $_nC_r$ で表す
● $nC_r$ の計算
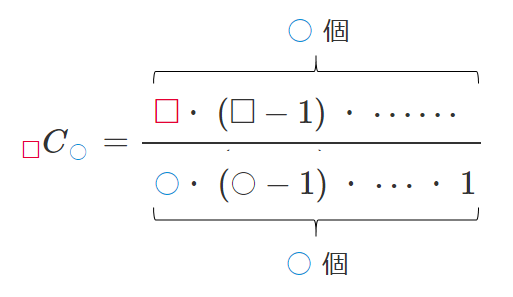
● $_nC_r$ の性質
$_nC_r=_nC_{n-r}$
計算が大変なときに使おう
問題
(1) 5人から2人選ぶ
(2) 7つの文字 $a~g$ から5つ選ぶ
(1) 5人から2人選ぶ
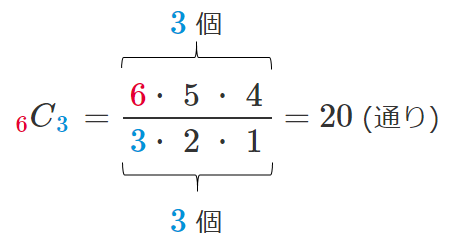
(2) 7つの文字 $a~g$ から5つ選ぶ
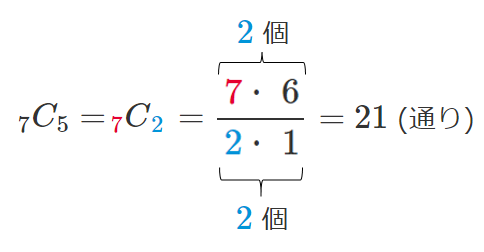

まずは計算に慣れることが大切!




コメント