高校数学で最初につまずくのは絶対値!
絶対値のおさえるべきポイントは
『絶対値の中の符号によって絶対値のはずし方が異なる』
ということ!
絶対値のはずし方をマスターして,絶対値の理解を深めよう!
この記事を読んだら,絶対値の基本はばっちり!

絶対値が苦手!

絶対値が苦手な人は多いよね!
絶対値の基本を復習しよう!
絶対値

絶対値って何か分かる?

正直よく分かっていない…

きちんと理解しないと問題は解けないよ!

絶対値が何か教えてください…

絶対値は原点からの距離を表す記号だよ!
例えば、$|2|$ は原点と点 $2$ の距離を表しているよ!
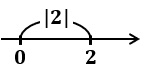

だから $|2|=2$ になるのか!

その通り!
絶対値の中が正のときは、
その数がそのまま距離になるから、
絶対値をそのままはずすだけでいいよ!

なるほど!
$\displaystyle{|\frac{1}{2}|}$ は原点と点 $\displaystyle{\frac{1}{2}}$ の距離だから $\displaystyle{\frac{1}{2}}$ になるし、
$\left|\sqrt{2}\right|$ は原点と点 $\sqrt{2}$ の距離だから $\sqrt{2}$ になるんだね!

$|-2|$ は何になるか分かる?

$|-2|$ は原点と点 $(-2)$ の距離だから $2$ になる!
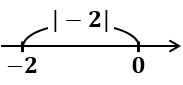

そうだね! $|-2|=2$ だね!
絶対値の中が負のときは、
マイナスがとれた数が原点からの距離になるんだ!
マイナスをとるためにマイナスをつけて絶対値をはずすと覚えておこう!
$|-2|=-(-2)=2$

なるほど!
絶対値の中が負のときは、
マイナスをつけて絶対値をはずせばいいんだね!

その通り!
$\displaystyle{\left|-\frac{1}{2}\right|=-(-\frac{1}{2})=\frac{1}{2}}$
$\left|-\sqrt{2}\right|=-(-\sqrt{2})=\sqrt{2}$
絶対値の中が正のときは 『そのまま』はずす
絶対値の中が負のときは 『マイナスをつけて』はずす
数式で表すと
例題1 次の絶対値を計算せよ。
(1) $|4|$
(2) $|-\frac{1}{3}|$
(3) $|\sqrt{2}-1|$
(4) $|1-\sqrt{3}|$
(1)
$|4|=4$
(2)
$\displaystyle{|-\frac{1}{3}|=-(-\frac{1}{3})=\frac{1}{3}}$
(3)
$1<\sqrt{2}<2$ より,$(\sqrt{2}-1)$ は正なので
$|\sqrt{2}-1|=\sqrt{2}-1$
(絶対値の中が正のときはそのままはずす)
(4)
$1<\sqrt{3}<2$ より,$(1-\sqrt{3})$ は負なので
$|1-\sqrt{3}|=-(1-\sqrt{3})=-1+\sqrt{3}$
(絶対値の中が負のときはマイナスをつけてはずす)
まとめ
● 絶対値は原点からの距離を表す記号である
● 絶対値をはずすときは絶対値の中の符号が大切である
絶対値の中が正のときは,『そのまま』はずす
絶対値の中が負のときは,『マイナスをつけて』はずす
● $|a|=\begin{cases}a & ( a≧0 ) \\ -a & ( a<0 )\end{cases}$
問題
問題1 次の絶対値を計算せよ。
(1) $|\frac{2}{3}|$
(2) $|-3|$
(3) $\left|\sqrt{5}-2\right|$
(4) $\left|3-\pi\right|$
解答
(1)
$$\displaystyle{|\frac{2}{3}|=\frac{2}{3}}$$
(2)
$|-3|=-(-3)=3$
(3)
$2<\sqrt{5}<3$ より,$(\sqrt{5}-2)$ は正なので
$\left|\sqrt{5}-2\right|=\sqrt{5}-2$
(絶対値の中が正のときはそのままはずす)
(4)
$\pi=3.14…$ より,$(3-\pi)$ は負なので
$\left|3-\pi\right|=-(3-\pi)=-3+\pi$
(絶対値の中が負のときはマイナスをつけてはずす)

絶対値のはずし方をマスターすれば絶対値の基本は完璧!
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント