苦手な高校生が多い『絶対値の方程式と不等式』
『絶対値』が『原点からの距離を表している』ことを使えば,
『絶対値の方程式と不等式』は簡単に理解することができる!
この記事を読めば,『絶対値の方程式と不等式』 は完璧!

絶対値の方程式と不等式を、解き方を覚えて解いているだけのような気がして…

それじゃあ、絶対値の等式と不等式の解き方をきちんと理解してみよう!
方程式 $|x|=c$ の解き方

絶対値って何だったかな?

原点からの距離!

その通り!
絶対値は『原点からの距離』を表す記号だということを頭に入れて絶対値の問題を解くようにしよう!
まずは絶対値の方程式から!
方程式 $|x|=1$ の答えは何かわかる?

$x=±1$
何となく解けるけど,なんでこの答えになるかよく分かってない…

それじゃあ,方程式 $|x|=1$ の答えが $x=±1$ になる理由をきちんと理解しよう!
$|x|$ は点 $x$ の原点からの距離
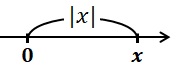
『方程式 $|x|=1$ を解く』とは
『$(点xの原点からの距離)=1$ になる $x$ の値を求める』ということ
原点からの距離が $1$ になる点は,
点 $1$ と点 $-1$ になる
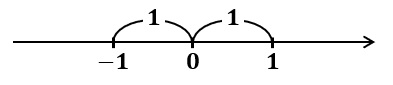
つまり,
方程式 $|x|=1$ を解くと、$x=±1$ になる
『方程式 $|x|=1$ を解く』という問題を
『原点からの距離が $1$ である $x$ の値を求める」
という問題に言い換えることができるようにしよう
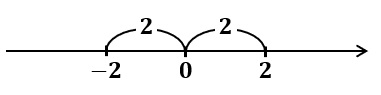
原点からの距離が $2$ である $x$ を求めるので
$x=±2$
不等式 $|x|<c$ の解き方

絶対値の方程式は理解できた!
不等式も同じように考えたら解ける?

絶対値の不等式も同じように数式の意味を理解すれば解けるよ!
『不等式 $|x|<1$ を解く』とは
『$(点xの原点からの距離)<1$ になる $x$ の値の範囲を求める』ということ
原点からの距離が $1$ より小さくなる値の範囲は
$-1$ と $1$ の間
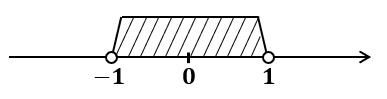
数式で表すと、$x$ の範囲は $-1<x<1$
つまり,
不等式 $|x|<1$ を解くと、$-1<x<1$ になる
『不等式 $|x|<1$ を解く』という問題を
『原点からの距離が $1$ より小さい $x$ の値の範囲を求める』
という問題に言い換えることができるようにしよう
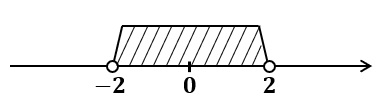
原点からの距離が$2$より小さい$x$の範囲を求めるので
$-2<x<2$
不等式 $|x|>c$ の解き方
『不等式 $|x|>1$ を解く』とは
『$(点xの原点からの距離)>1$ になる $x$ の値の範囲を求める』ということ
原点からの距離が $1$ より大きくなる値の範囲は,
$-1$ より小さい値と $1$ より大きい値になる
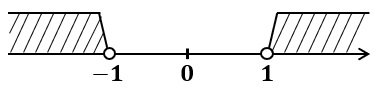
数式で表すと,$x$ の値の範囲は $x<-1,1<x$
つまり,
不等式 $|x|>1$ を解くと,$x<-1,1<x$ になる
『不等式 $|x|>1$ を解く』という問題を
『原点からの距離が$1$より大きい$x$の範囲を求める』
という問題に言い換えることができるようにしよう
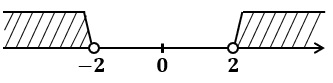
原点からの距離が$2$より大きい$x$の範囲を求めるので
$x<-2,2<x$
数直線と不等式の関係
数直線を作れば、不等式は簡単に作れるということを知っておこう
数直線における大小関係は必ず以下のようになる
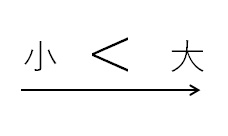
右にいけばいくほど大きい値になるので、大小関係は『$<$』の不等号で表すことができる
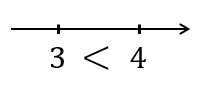
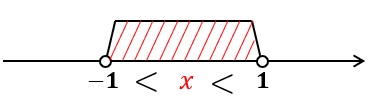
斜線部が $x$ のとりうる値の範囲なので,斜線部に $x$ を書くと不等式が簡単に作れる
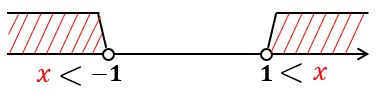
問題
(1) $|x|=3$
(2) $|x|≦3$
(3) $|x|>3$
(4) $|x|=-1$
解答
(1) $|x|=3$
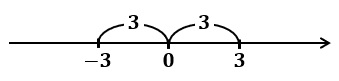
原点からの距離が $3$ である $x$ を求めるので
$x=±3$
(2) $|x|≦3$

原点からの距離が $3$ 以下の $x$ の値の範囲を求めるので
$-3≦x≦3$
(3) $|x|>3$
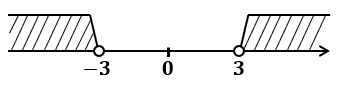
原点からの距離が $3$ より大きい $x$ の範囲を求めるので
$x<-3,3<x$
(4) $|x|=-1$
原点からの距離が $-1$ である $x$ は存在しないので
解はない

覚えて解くのではなく、
数式を理解して解けるようにしよう!
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント