重複順列 | シグにゃんの数学ブログ

重複順列とは

普通の順列と何が違うのかな？

普通の順列は，異なるものだけを並べる順列を考えてきた！

「重複順列」とは，同じものを使うことを許した順列のこと！

順列の復習はこれ↓

重複順列とは

同じものを使うことを許した順列
重複してもいい順列（かぶってもよい）

具体例を使って重複順列を考えてみよう！

２つの数字 $1，2$ を重複を許して並べて４桁の整数を作るとき，何個の整数が作れるか

樹形図をかくと　$16$ 通り

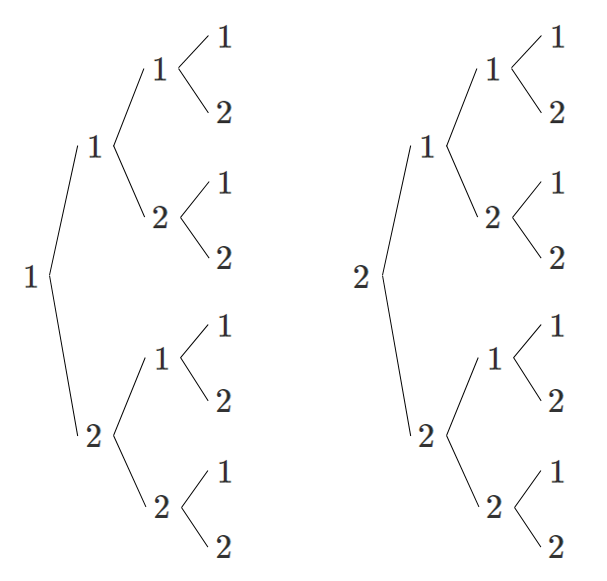
【考え方】

千の位は $1$ または $2$ の $2$ 通り
百の位も $1$ または $2$ の $2$ 通り
十の位も $1$ または $2$ の $2$ 通り
一の位も $1$ または $2$ の $2$ 通り

重複が許されているので，各位とも $2$ 通りになる

積の法則より　$2×2×2×2=16$ (通り)

$2$ 個のものを重複を許して $4$ 個並べる順列は，$2^4$ で計算できる！

３つの数字 $1，2，3$ を重複を許して並べて４桁の整数を作るとき，何個の整数が作れるか

重複が許されているので，各位とも $3$ 通りになる

積の法則より　$3×3×3×3=81$ (通り)

$3$ 個のものを重複を許して $4$ 個並べる順列は，$3^4$ で計算できる！

異なる $n$ 種類のものから重複を許して $r$ 個取って並べる順列を

$n$ 個から $r$ 個取る重複順列

という

重複順列の総数

$n$ 個から $r$ 個取る重複順列の総数は $n^r$

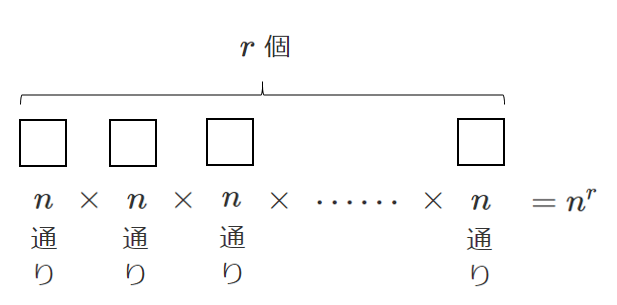
$r^n$ と間違えないように！

上のような図を描いて問題を整理しよう！

● 重複順列とは

　同じものを使うことを許した順列
　重複してもいい順列（かぶってもよい）

● 重複順列の総数

　$n$ 個から $r$ 個取る重複順列の総数は $n^r$

次の場合の数を求めよ。
(1)　４個の文字 $a，b，c，d$ を，重複を許して３個だけ１列に並べる
(2)　６人を２つの部屋 $A，B$ に分ける（１人も入らない部屋があってもよい）

(1)　４個の文字 $a，b，c，d$ を，重複を許して３個だけ１列に並べる

　$4^3=64$ (通り)

□に入るのはそれぞれ $a，b，c，d$ の４通り

(2)　６人を２つの部屋 $A，B$ に分ける（１人も入らない部屋があってもよい）

　$2^6=64$ (通り)

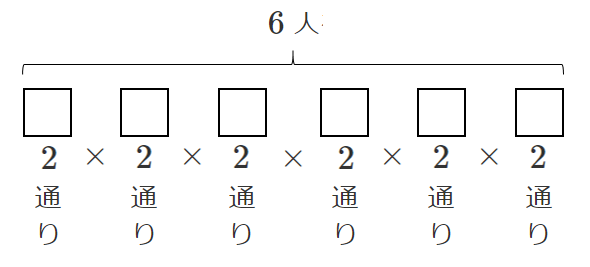
□に入るのはそれぞれ $A，B$ の２通り

図に表すことで式を作りやすいよ！