
導関数を調べれば,関数の増減が分かる!
3次関数のグラフをかこう!
導関数と接線の傾きの関係
$f(x)$ を微分した関数が導関数 $f'(x)$
導関数 $f'(x)$ に $x=a$ を代入すると
$x=a$ における微分係数
である
$x=a$ における微分係数は
関数 $f(x)$ 上の点 $(a,f(a))$ における接線の傾き
と等しい
微分係数と接線の傾きの関係はこれ↓

関数の増減と接線の傾き
関数が増加する …… 接線の傾きが正

関数が減少する …… 接線の傾きが負

関数の増減と導関数
接線の傾きは,導関数 $f'(x)$ なので
関数 $f(x)$ が増加する …… 接線の傾きが正
すなわち
関数 $f(x)$ が増加する …… 導関数 $f'(x)>0$

関数 $f(x)$ が減少する …… 接線の傾きが負
すなわち
関数 $f(x)$ が減少する …… 導関数 $f'(x)<0$
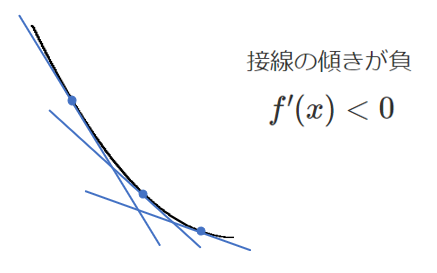
$f'(x)<0$ となる $x$ の値の範囲では $f(x)$ は減少する
3次関数のグラフ

関数 $f(x)$ の増減と $f'(x)$ の符号の関係を使って,3次関数のグラフをかいてみよう!
● 導関数 $f'(x)$ を求める
$f'(x)=3x^2-3=3(x^2-1)=3(x+1)(x-1)$

因数分解できたら因数分解しておくことがポイント!
● 導関数 $f'(x)$ の符号を調べる
$f'(x)=0$ のとき $3(x+1)(x-1)=0$
$x=±1$
$f'(x)$ のグラフをかくと
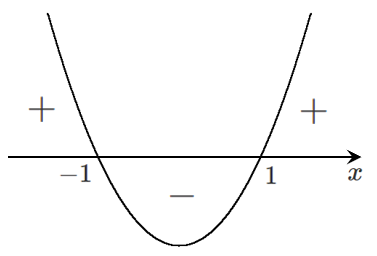
- $f'(x)=3x^2-3$ は2次関数
- $f'(x)=0$ の解 $x=±1$ は $f'(x)$ と $x$ 軸の共有点
- $x$ 軸より上側の範囲が $f'(x)>0$ すなわち $x<-1,1<x$
- $x$ 軸より下側の範囲が $f'(x)<0$ すなわち $-1<x<1$

$x$ 軸と $f'(x)$ のグラフをかいて,
・共有点の座標
・$x$ 軸より上側なら $+$
・$x$ 軸より下側なら $-$
を書き込もう!
● 増減表をかく
手順① 表をつくる

手順② $x$ の行に $f'(x)=0$ の解 $x=±1$ をかく
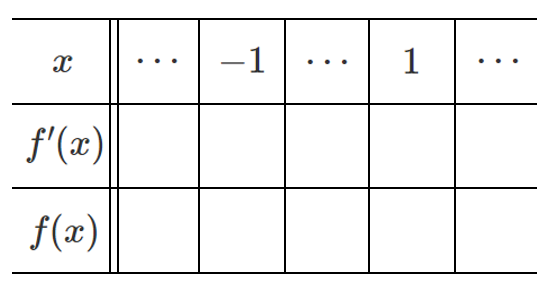
手順③ $f'(x)$ の行に $0$,$+$,$-$ をかく
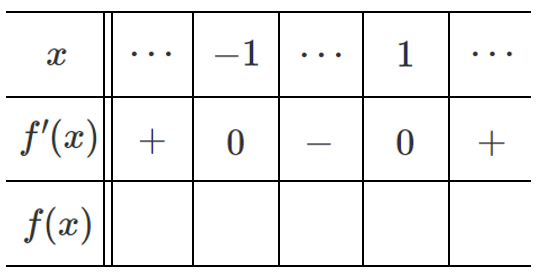
$f'(x)$ のグラフをもとに表に書き込む

手順④ $f(x)$ の行をかく
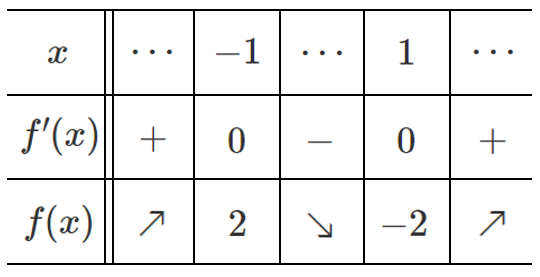
$f'(x)$ が $+$ のときは,$f(x)$ は増加するので ↗ をかく
$f'(x)$ が $-$ のときは,$f(x)$ は減少するので ↘ をかく
$f(x)=x^3-3x$ より
$f(-1)=(-1)^3-3\cdot(-1)=2$
$f(1)=1^3-3\cdot1=-2$

増減表は上の行から順番に書き込んでいこう!
● 増減表の $f(x)$ の行をみてグラフをかく
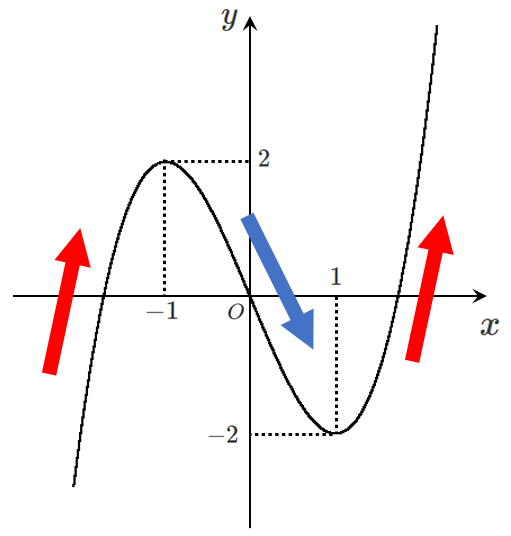
導関数を求めると
$f'(x)=-3x^2+3=-3(x^2-1)=-3(x+1)(x-1)$
$f'(x)=0$ のとき
$x=±1$
$f'(x)$ のグラフをかくと
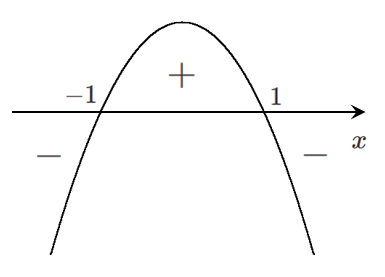
増減表をかくと
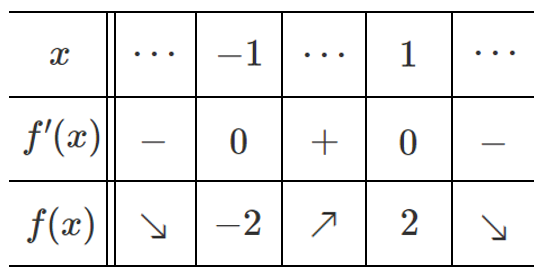
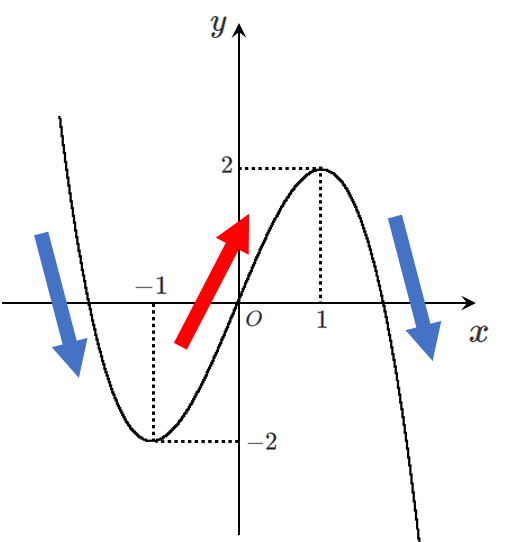
グラフをかくと
まとめ
● 導関数と接線の傾きの関係
導関数 $f'(x)$ は関数 $f(x)$ 上の点における接線の傾きを表している
● 関数の増減と接線の傾き
関数が増加する …… 接線の傾きが正

関数が減少する …… 接線の傾きが負

● 関数 $f(x)$ の増減と導関数 $f'(x)$ の符号
$f'(x)>0$ となる $x$ の値の範囲では $f(x)$ は増加する
$f'(x)<0$ となる $x$ の値の範囲では $f(x)$ は減少する

関数の増減と導関数の符号の関係をきちんと理解してグラフをかけるようにしよう!




コメント