
関数の極大・極小とは何か?
詳しく学ぼう!
関数の極大・極小
3次関数 $f(x)=x^3-3x$ のグラフは以下のようになる
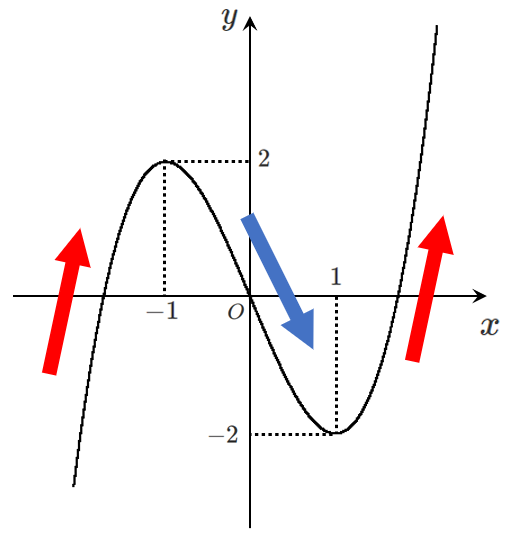
$x=-1$ を境目にして増加から減少に移るとき,
$x=-1$ で極大である
$x=-1$ で極大値 $2$ をとる
という
$x=1$ を境目にして減少から増加に移るとき,
$x=1$ で極小である
$x=1$ で極小値 $-2$ をとる
という
極大値と極小値をまとめて 極値 という
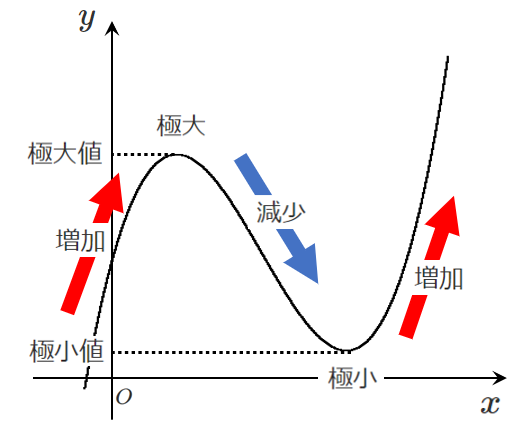

増加と減少が入れかわるところが極値となる!
常に増加,常に減少する場合は極値をもたない!
常に増加,常に減少する場合は極値をもたない
3次関数の極大・極小

問題を解いてみよう!
導関数 $f'(x)$ を求めると
$f'(x)=3x^2-6x=3x(x-2)$
$f'(x)=0$ を求めると
$3x(x-2)=0$
$x=0,2$
$f'(x)$ のグラフをかくと
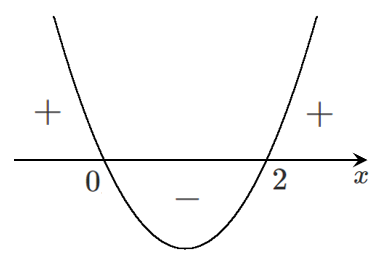
増減表をかくと
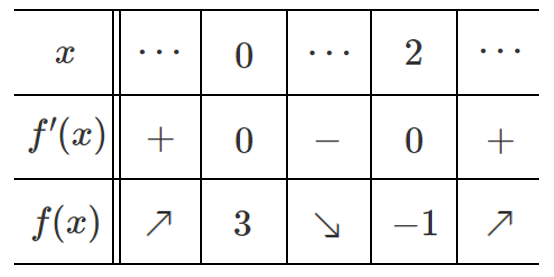
したがって
$x=0$ で極大値 $3$
$x=2$ で極小値 $-1$
グラフは
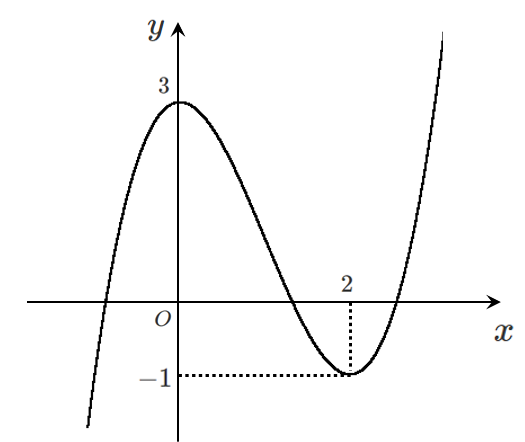
増減表で極値は求まるので,グラフはかかなくてもよい
導関数 $f'(x)$ を求めると
$f'(x)=-3x^2+6x=-3x(x-2)$
$f'(x)=0$ を求めると
$-3x(x-2)=0$
$x=0,2$
$f'(x)$ のグラフをかくと
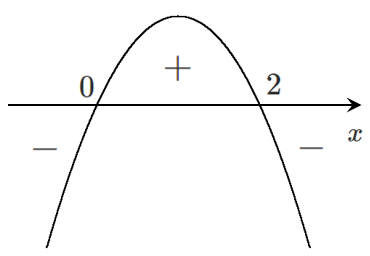
増減表をかくと
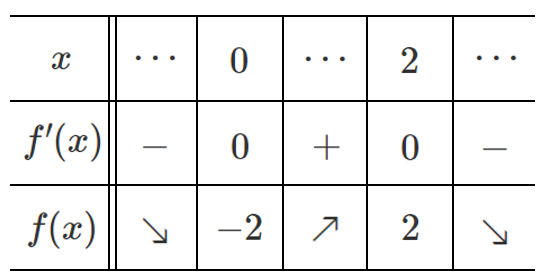
したがって
$x=2$ で極大値 $2$
$x=0$ で極小値 $-2$
グラフは
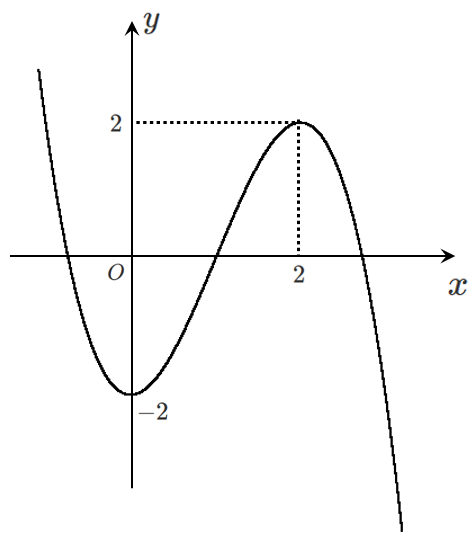
増減表で極値は求まるので,グラフはかかなくてもよい
極値をもたない場合

関数によっては極値をもたない場合もある!
極値をもたない関数についても考えてみよう!
導関数 $f'(x)$ を求めると
$f'(x)=3x^2$
$f'(x)=0$ を求めると
$3x^2=0$
$x=0$
$f'(x)$ のグラフをかくと
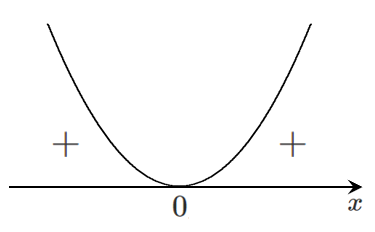
増減表をかくと
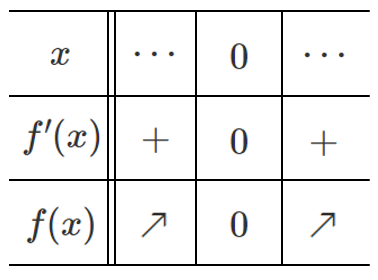
関数 $f(x)$ は常に増加する
つまり,増減が入れかわらないので
$f(x)$ は極値をもたない
グラフは
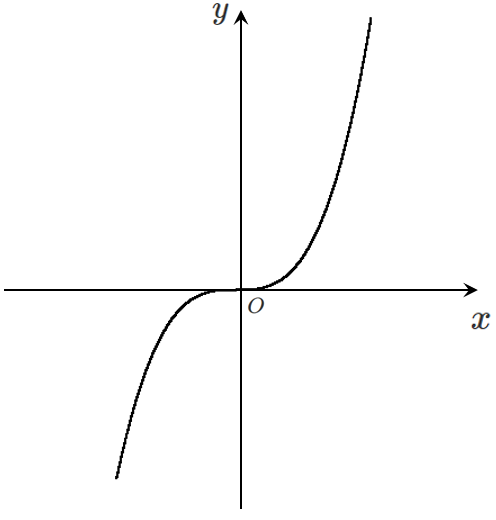

常に増加するから極値をもたない!
導関数 $f'(x)$ を求めると
$f'(x)=-3x^2-1$
$f'(x)=0$ を求めると
$3x^2=-1$
この方程式は実数解をもたない
$f'(x)$ のグラフをかくと
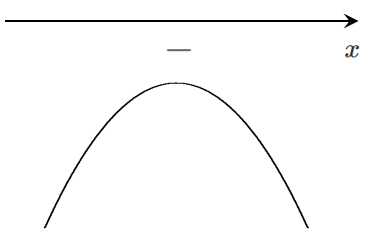
$f'(x)=0$ が実数解をもたないので,$f'(x)$ は $x$ 軸と共有点をもたない
増減表をかくと
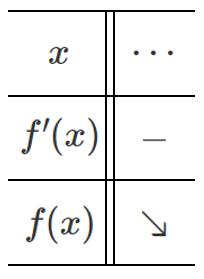
関数 $f(x)$ は常に減少する
つまり,増減が入れかわらないので
$f(x)$ は極値をもたない
グラフは
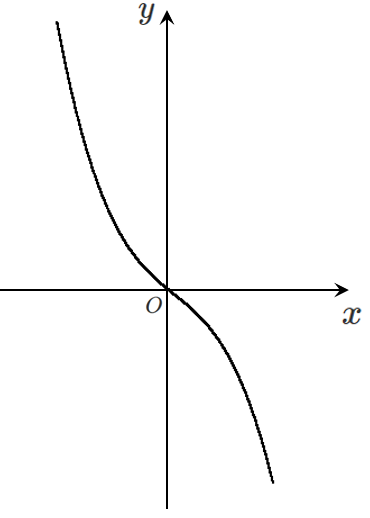

常に減少するから極値をもたない!
まとめ
● 関数の極大・極小

増加から減少に入れかわるところを極大
減少から増加に入れかわるところを極小
● 極値をもたない場合
関数が 常に増加する または 常に減少する ときは
増減が入れかわらないので極値をもたない

極値を確実に求められるようにしよう!

極値をもたない場合もおさえておこう!




コメント