階差数列
$1,3,7,13,21,\cdots\cdots$
という数列について,隣り合う $2$ 項の差とると
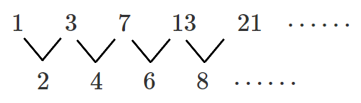
$2,4,6,8,\cdots\cdots$ という数列が得られる
この $2,4,6,8,\cdots\cdots$ を $1,3,7,13,21,\cdots\cdots$ の 階差数列 とよぶ
数列 $\{a_n\}$ の隣り合う $2$ 項の差
$a_{n+1}-a_n=b_n$ ($n=1,2,3,\cdots\cdots$)
を項とする数列 $\{b_n\}$ を,数列 $\{a_n\}$ の 階差数列 という
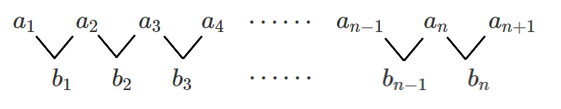
階差数列から一般項を求める方法
$1,3,7,13,21,\cdots\cdots$
は等差数列でも等比数列でもないので,このままでは一般項を求めることができない
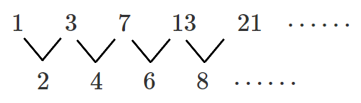
しかし,階差数列をとることで,一般項を求めることができる
数列 $\{a_n\}$ とその階差数列 $\{b_n\}$ について
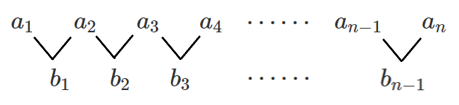
$a_2=a_1+$$b_1$
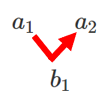
$a_3=a_2+b_2=(a_1+b_1)+b_2=a_1+$$b_1+b_2$
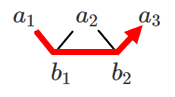
$a_4=a_3+b_3=(a_1+b_1+b_2)+b_3=a_1+$$b_1+b_2+b_3$
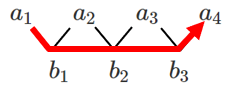
したがって,$n≧2$ のとき
$a_n=a_1+$$b_1+b_2+b_3+\cdots\cdots+b_{n-1}$
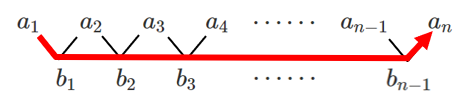
これをΣを用いて表すと
$\displaystyle{a_n=a_1+\sum_{k=1}^{n-1}b_k}$
数列 $\{a_n\}$ の階差数列を $\{b_n\}$ とすると
$n≧2$ のとき $\displaystyle{a_n=a_1+\sum_{k=1}^{n-1}b_k}$
「$n≧2$ のとき」というのはとても重要
$n=1$ のとき,すなわち $a_1$ は,階差数列を使って表すことができない
また,$n=1$ を上の式に代入すると
$\displaystyle{a_1=a_1+\sum_{k=1}^{0}b_k}$
となり,Σの式があり得ない式になってしまう
よって,上の式を用いる場合は 「$n≧2$ のとき」 と書く必要がある

$\{a_n\}$ の初項と階差数列 $\{b_n\}$ の初項から第 $(n-1)$ 項までの和で $\{a_n\}$ の一般項が求まるんだね!

第 $(n-1)$ 項までというところがポイント!
間違えないようにしよう!
Σが苦手な人はこれ↓

問題

問題を解いてみよう!
次の数列 $\{a_n\}$ の一般項を求めよ。
(1) $1,3,8,16,27,\cdots\cdots$
(2) $2,3,5,9,17,\cdots\cdots$
(1) $1,3,8,16,27,\cdots\cdots$
この数列の階差数列 $\{b_n\}$ は
$2,5,8,11,\cdots\cdots$
数列 $\{b_n\}$ は初項 $2$,公差 $3$ の等差数列なので
$b_n=2+3(n-1)=3n-1$
$n≧2$ のとき
\begin{eqnarray} a_n &=& a_1+\sum_{k=1}^{n-1}(3k-1) \\\\ &=& 1+3\cdot\frac{1}{2}(n-1)\{(n-1)+1\}-(n-1) \\\\ &=& 1+\frac{3}{2}n(n-1)-(n-1) \\\\ &=& \frac{3}{2}n^2-\frac{5}{2}n+2 \\\\ \end{eqnarray}$n=1$ を代入すると $a_1=1$
よって,$\displaystyle{a_n=\frac{3}{2}n^2-\frac{5}{2}n+2}$ は $n=1$ のときも成り立つ
したがって, $\displaystyle{a_n=\frac{3}{2}n^2-\frac{5}{2}n+2}$
(2) $2,3,5,9,17,\cdots\cdots$
この数列の階差数列 $\{b_n\}$ は
$1,2,4,8,\cdots\cdots$
数列 $\{b_n\}$ は初項 $1$,公比 $2$ の等比数列なので
$b_n=2^{n-1}$
$n≧2$ のとき
\begin{eqnarray} a_n &=& a_1+\sum_{k=1}^{n-1}2^{k-1} \\\\ &=& 2+\frac{2^{n-1}-1}{2-1} \\\\ &=& 2+2^{n-1}-1 \\\\ &=& 2^{n-1}+1 \\\\ \end{eqnarray}$n=1$ を代入すると $a_1=2$
よって,$a_n=2^{n-1}+1$ は $n=1$ のときも成り立つ
したがって, $a_n=2^{n-1}+1$
Σの計算が苦手な人はこれ↓
まとめ
● 階差数列
数列 $\{a_n\}$ の隣り合う $2$ 項の差
$a_{n+1}-a_n=b_n$ ($n=1,2,3,\cdots\cdots$)
を項とする数列 $\{b_n\}$ を,数列 $\{a_n\}$ の 階差数列 という
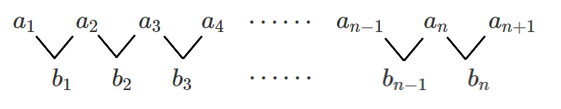
● 階差数列から一般項を求める
数列 $\{a_n\}$ の階差数列を $\{b_n\}$ とすると
$n≧2$ のとき $\displaystyle{a_n=a_1+\sum_{k=1}^{n-1}b_k}$

階差数列は差がつくところ!
きちんと解けるようにしよう!




コメント