順列
順列 … いくつかのものを一列に並べたもの

「樹形図」を用いて順列の考え方をマスターしよう!
樹形図の復習はこれ↓

樹形図をかくと
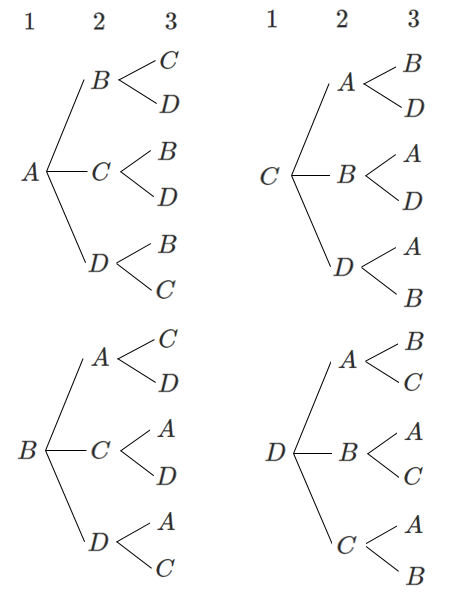
1番目は $A$,$B$,$C$,$D$ の $4$ 通り
そのどの場合に対しても,2番目は
1番目を抜いた $3$ 通り
そのどの場合に対しても,3番目は
1,2番目を抜いた $2$ 通り
積の法則より $4×3×2=24$ (通り)
積の法則の復習はこれ↓

1番目は $A$,$B$,$C$,$D$,$E$ の $5$ 通り
そのどの場合に対しても,2番目は
1番目を抜いた $4$ 通り
そのどの場合に対しても,3番目は
1,2番目を抜いた $3$ 通り
積の法則より $5×4×3=60$ (通り)
$_nP_r$
異なる $n$ 個のものから異なる $r$ 個を取り出して並べる順列を
$n$ 個から $r$ 個取る順列 という
その総数を $_nP_r$ で表す
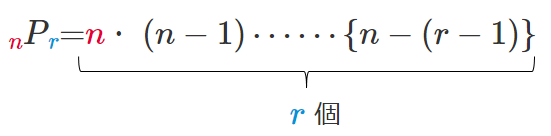
※ $P$ は「順列」を表す「permutation」の頭文字

順列の具体例を見てみよう!
$4$ 個の文字 $A$,$B$,$C$,$D$ から異なる $3$ 個をとって1列に並べる
$4$ 個から $3$ 個取る順列 … $_4$$P$$_3$
その計算が $4×3×2$ なので
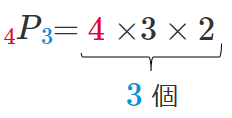
$5$ 個の文字 $A$,$B$,$C$,$D$,$E$ から異なる $3$ 個をとって1列に並べる
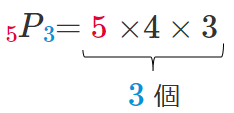
$5$ 個から $3$ 個取る順列 … $_5$$P$$_3$
その計算が $5×4×3$ なので
$6$ 個から $4$ 個取る順列なので
$_6P_4=6×5×4×3=360$ (通り)
$n!$
$_nP_n$ ($n$ 個から $n$ 個をとって並べる順列)のことを $n!$ と表す
$n!=n・(n-1)・(n-2)・\cdots\cdots・3・2・1$
異なる $n$ 個すべてを並べる順列の総数 … $n!$
※「!」は「階乗」と読む
$6!=6・5・4・3・2・1=720$ (通り)
まとめ
● $_nP_r$
異なる $n$ 個から異なる $r$ 個取る順列の総数 … $_nP_r$

● $n!$
異なる $n$ 個すべてを並べる順列の総数 … $n!$
$n!=n・(n-1)・(n-2)・\cdots\cdots・3・2・1$
問題
(1) 7人から3人を選んで1列に並べる
(2) $1~9$ の9つから異なる3個を並べてできる3桁の整数
(3) $A~E$ の5個の文字をすべて並べる
(1) 7人から4人を選んで1列に並べる
$_7P_4=7・6・5・4=840$ (通り)
(2) $1~9$ の9つから異なる3個を並べてできる3桁の整数
$_9P_3=9・8・7=504$ (通り)
(3) $A~E$ の5個の文字をすべて並べる
$5!=5・4・3・2・1=120$ (通り)

選んで並べる問題は $_nP_r$ を使う!




コメント