高校数学Ⅱで学ぶ『高次方程式の虚数解』についてわかりやすく解説しました!
今回の投稿で扱う問題は、数学Ⅱの複素数の範囲の理解度を確認するにはちょうどよい問題です!
この投稿を見れば、複素数の内容の総復習ができます!
問題
「3次方程式の解の1つが $1+2i$」という条件から、この問題の解答の方針として2種類考えられる。
② $1+2i$ の共役な複素数 $1-2i$ も解である(解答2)(解答3)
①については、「解である➡代入」というシンプルな発想である。
②については、「実数係数の方程式の虚数解が与えられたときは、共役な複素数も解である」という性質を利用している。
3次方程式の解の種類を考えると
(1次式)(1次式)(1次式)=0 … 異なる3つの実数解
(1次式)(1次式)²=0 … 異なる2つの実数解(片方は $2$ 重解)
(1次式)³=0 … 1つの実数解( $3$ 重解)
(1次式)(2次式)=0 … 異なる3つの実数解 または 1つの実数解と異なる2つの虚数解
3次方程式で虚数解が解になるのは、(1次式)(2次式)=0 という形に変形され、(2次式)=0(2次方程式)の解として互いに共役な虚数解が出てくる場合である。
今回の問題における3次方程式の解の1つが $1+2i$ の場合は、共役な複素数 $1-2i$ も解となる。
そして、3次方程式は (1次式)(2次式)=0 と変形され、1つの実数解と異なる2つの虚数解(互いに共役)という解になる。

解答1|代入と複素数の相等
● $1+2i$ が解 ➡ 代入
● $○+□i=0$ と式変形 ➡ $○$ と $□$が実数なら $○=0$,$□=0$
$1+2i$ が解であるから
$(1+2i)^3+a(1+2i)+b=0$
$(1+6i+12i^2+8i^3)+a(1+2i)+b=0$
$(1+6i-12-8i)+a(1+2i)+b=0$
$(a+b-11)+(2a-2)i=0$
$a$,$b$ は実数であるから,$a+b-11$,$2a-2$ は実数である
よって $a+b-11=0$,$2a-2=0$
これを解くと $a=1$,$b=10$
このときの方程式は $x^3+x+10=0$
左辺を因数分解すると $(x+2)(x^2-2x+5)=0$
したがって $x=-2,1\pm2i$
以上より $a=1$,$b=10$,他の解は $-2$,$1-2i$
解答2|与えられた解をもつ2次方程式で割る
● 実数係数の方程式において $1+2i$ が解 ➡ 共役な複素数 $1-2i$ も解
● $x^2-(解の和)x+(解の積)=0$ を用いる
➡ $1\pm2i$ を解にもつ2次方程式 $x^2-2x+5=0$ が求まる
● $x^3+ax+b=0$ が $(1次式)(x^2-2x+5)=0$ と変形される
➡ $x^3+ax+b$ は $x^2-2x+5$ で割り切れる
係数がすべて実数であるから,$1+2i$ と共役な複素数 $1-2i$ も解である
$1+2i$ と $1-2i$ を解にもつ2次方程式の1つは
$x^2-\{(1+2i)+(1-2i)\}x+(1+2i)(1-2i)=0$
すなわち $x^2-2x+5=0$
よって,$x^3+ax+b$ は $x^2-2x+5$ で割り切れる
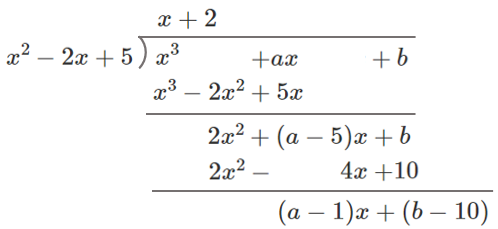
商は $x+2$,余りは $(a-1)x+(b-10)$
この余りは $0$ になるから $a-1=0$,$b-10=0$
これを解くと $a=1$,$b=10$
このときの方程式は $(x+2)(x^2-2x+5)=0$
これを解くと $x=-2,1\pm2i$
したがって $a=1$,$b=10$,他の解は $-2$,$1-2i$
解答3|3次方程式の解と係数の関係
● 実数係数の方程式において $1+2i$ が解 ➡ 共役な複素数 $1-2i$ も解
● 残り1つの解を $\alpha$ とおく
➡ 3次方程式の解と係数の関係
$ax^3+bx^2+cx+d=0$ の解 $\alpha$,$\beta$,$\gamma$ とすると
$\displaystyle{\alpha+\beta+\gamma=-\frac{b}{a}}$
$\displaystyle{\alpha\beta+\beta\gamma+\gamma\alpha=\frac{c}{a}}$
$\displaystyle{\alpha\beta\gamma=-\frac{d}{a}}$
係数がすべて実数であるから,$1+2i$ と共役な複素数 $1-2i$ も解である
残りの解を $\alpha$ とすると,3次方程式の解と係数の関係より
$(1+2i)+(1-2i)+\alpha=0$ … ①
$(1+2i)(1-2i)+(1-2i)\alpha+\alpha(1+2i)=a$ … ②
$(1+2i)(1-2i)\alpha=-b$ …③
①より,$2+\alpha=0$ であるから $\alpha=-2$
②より,$5+(1-2i)(-2)+(-2)(1+2i)=a$ であるから $a=1$
③より,$5\cdot(-2)=-b$ であるから $b=10$
したがって $a=1$,$b=10$,他の解は $-2$,$1-2i$




コメント