高校数学Ⅱで学ぶ『座標平面における2つの円の位置関係』について解説!
2つの円の位置関係は5種類で、「中心間の距離」「半径の和」「半径の差」で決まります!
この投稿を見れば、『座標平面における2つの円の位置関係』はバッチリ!
2つの円の位置関係

2つの円の位置関係は5種類!
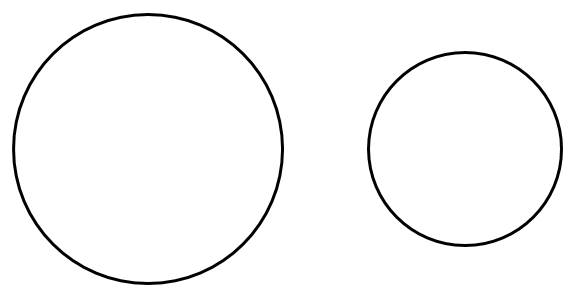
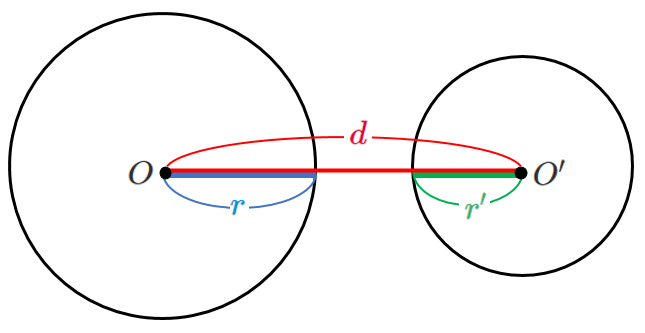
[1] 互いに外部にある
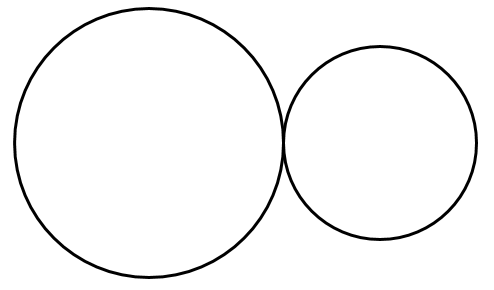
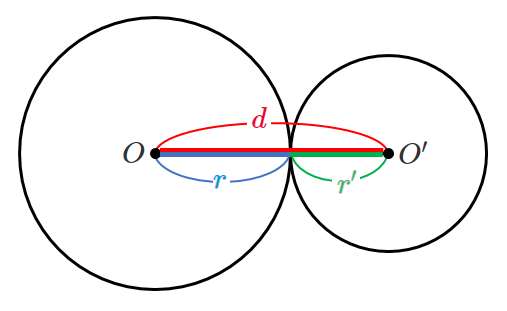
[2] 外接する
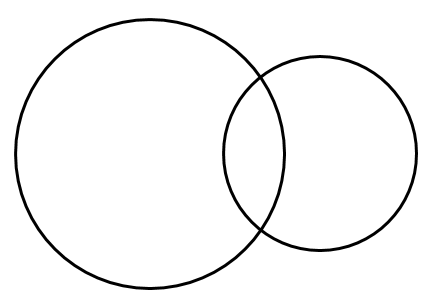
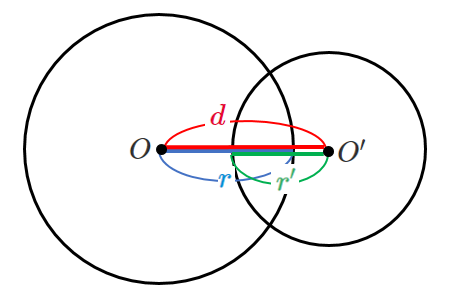
[3] 2点で交わる
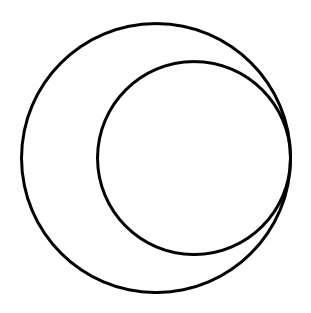
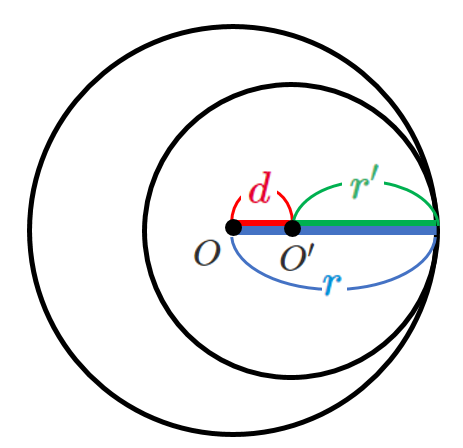
[4] 内接する
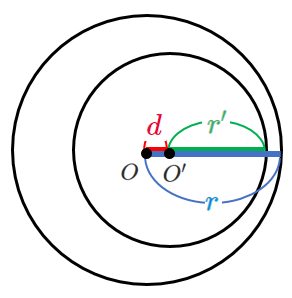
[5] 一方が他方の内部にある
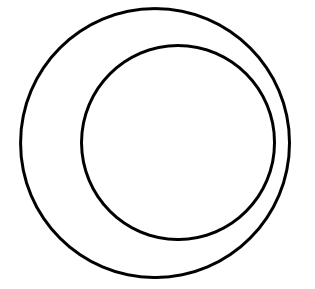

[1] から [5] になるにつれて,2つの円の中心が近づいているね!
図をかけば,5種類の位置関係はわかる!

2つの円の位置関係は,『中心間の距離』と『半径の和』と『半径の差』で決まるよ!
2つの円が外接する
2つの円が外接するとき $d=r+r’$ が成り立つ
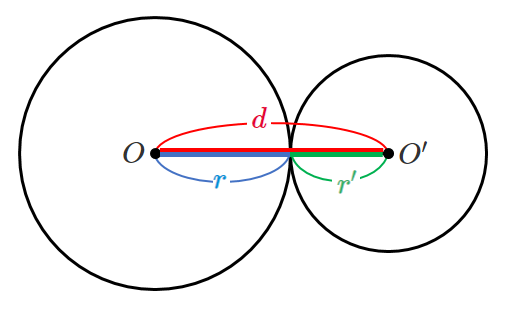

外接するときは,中心間の距離が「半径の和」と等しい!
円 $(x+2)^2+(y-2)^2=9$ の中心は $(-2,2)$,半径は $3$
中心間の距離 $d$ は
$d=\sqrt{(-2-1)^2+(-2-2)^2}$ 点と点の距離
$=\sqrt{25}$
$=5$
2つの円が外接するとき,中心間の距離が半径の和と等しいので,
求める円の半径を $r$ とすると
$r+3=5$
$r=2$
求める円の方程式は $(x-1)^2+(y+2)^2=4$
2つの円が内接する
2つの円が内接するとき $d=r-r’$ が成り立つ($r>r’$ のとき)
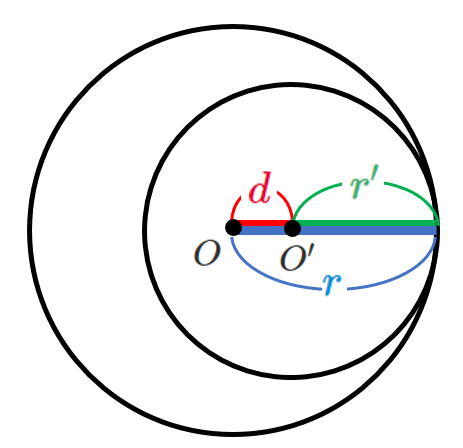

内接するときは,中心間の距離が「半径の差」と等しい!
円 $(x+2)^2+(y-2)^2=9$ の中心は $(-2,2)$,半径は $3$
中心間の距離 $d$ は
$d=\sqrt{(-2-1)^2+(-2-2)^2}$
$=\sqrt{25}$
$=5$
2つの円が内接するとき,中心間の距離が半径の差と等しいので,
求める円の半径を $r$ とすると
$r-3=5$
$r=8$
求める円の方程式は $(x-1)^2+(y+2)^2=64$
その他の位置関係

その他の位置関係は,「外接」と「内接」を基準に考えたら簡単だよ!
[1] 互いに外部にある
「外接する($d=r+r’$)」ときよりも中心間の距離 $d$ が大きい
すなわち $d>r+r’$
[5] 一方が他方の内部にある
「内接する($d=r-r’$)」ときよりも中心間の距離 $d$ が小さい
すなわち $d<r-r’$
[3] 2点で交わる
「内接する($d=r-r’$)」ときよりも中心間の距離 $d$ が大きい
「外接する($d=r+r’$)」ときよりも中心間の距離 $d$ が小さい
すなわち $r-r'<d<r+r’$

「外接」と「内接」をきちんとおさえておけば,その他の位置関係の式も分かるね!
円 $(x-2)^2+(y+1)^2=4$ は中心 $(2,-1)$,半径 2
円 $(x-1)^2+(y-1)^2=9$ は中心 $(1,1)$,半径 3
中心間の距離の距離は
$\sqrt{(2-1)^2+(-1-1)^2}=\sqrt{5}$
半径の差は $3-2=1$
半径の和は $3+2=5$
$1<\sqrt{5}<5$ すなわち (半径の差)<(中心間の距離)<(半径の和) より
2つの円は2点で交わる
まとめ
● 2つの円の位置関係
[1] 互いに外部にある
[2] 外接する
[3] 2点で交わる
[4] 内接する
[5] 一方が他方の外部にある
● 2つの円が外接する場合
$(中心間の距離)=(半径の和)$
● 2つの円が内接する場合
$(中心間の距離)=(半径の差)$
● 2つの円の位置関係と式
[1] 互いに外部にある
$(中心間の距離)>(半径の和)$
[2] 外接する
$(中心間の距離)=(半径の和)$
[3] 2点で交わる
$(半径の差)<(中心間の距離)<(半径の和)$
[4] 内接する
$(中心間の距離)=(半径の差)$
[5] 一方が他方の外部にある]
$(中心間の距離)<(半径の差)$
[1] から [5] につれて,中心間の距離は小さくなる
「外接」「内接」を基準に,[1] と [3] と [5] をおさえよう

2つの円の位置関係に関する問題は
『中心間の距離』と『半径の和』と『半径の差』の大小を考えよう!




コメント