2つの円の共通接線
2つの円の両方に接する接線を 共通接線 という

5種類の2つの円の位置関係について,共通接線の本数を見てみよう!
[1] 互いに外部にある
共通接線4本
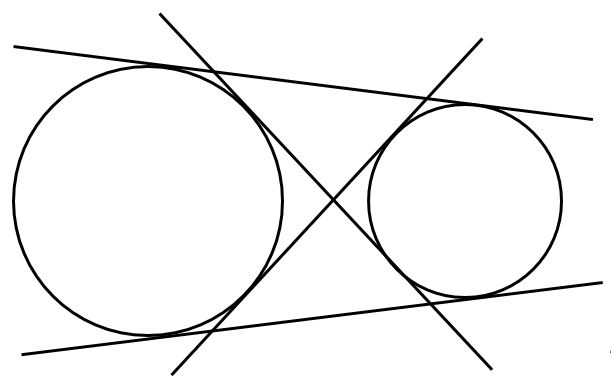
[2] 外接する
共通接線3本
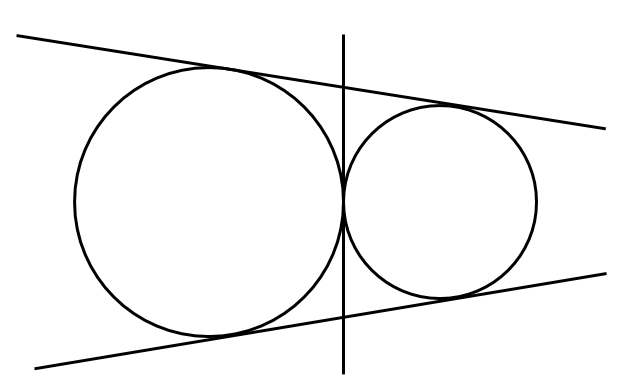
[3] 2点で交わる
共通接線2本
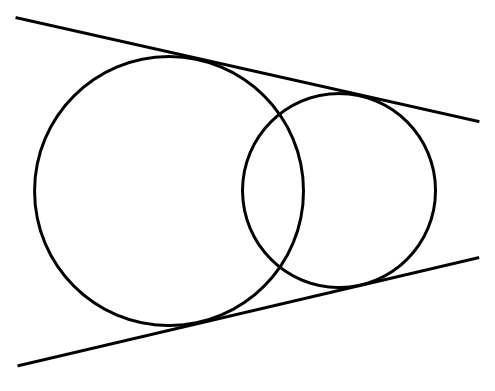
[4] 内接する
共通接線1本
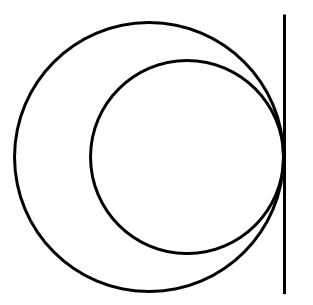
[5] 一方が他方の内部にある
共通接線なし

円の位置関係によって,共通接線の本数が変わるね!
2つの円の共通接線に関する問題
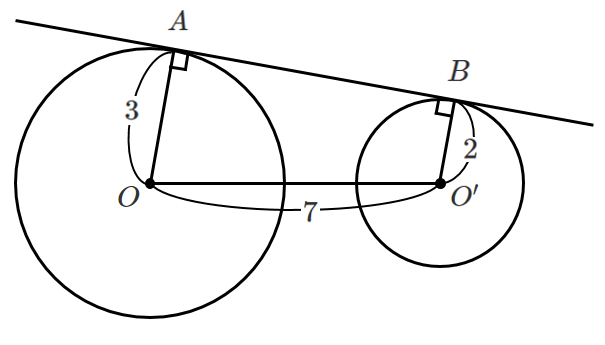
$O’$ から線分 $OA$ に垂線 $O’H$ を下ろすと
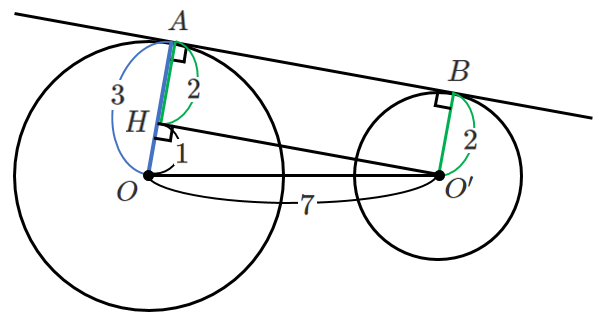
四角形 $ABO’H$ は長方形になるので
$AB=O’H$,$AH=BO’=2$
よって $OH=AO-AH=3-2=1$
$\triangle OO’H$ で三平方の定理より
$O’H^2=OO’^2-OH^2$
$=7^2-1^2$
$=48$
$O’H>0$ より $O’H=4\sqrt{3}$
$AB=O’H$より $AB=4\sqrt{3}$

垂線を下ろすところがポイント!
あとは直角三角形で三平方の定理!
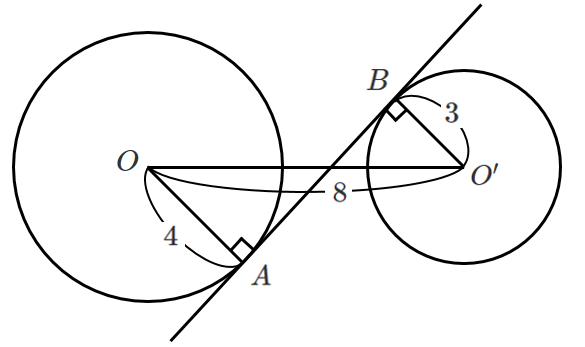
$O’$ から直線 $OA$ に垂線 $O’H$ を下ろすと
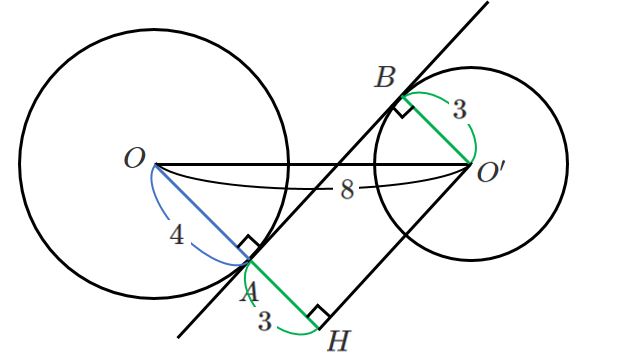
四角形 $ABO’H$ は長方形になるので
$AB=O’H$,$AH=BO’=3$
よって $OH=OA+AH=4+3=7$
$\triangle OO’H$ で三平方の定理より
$O’H^2=OO’^2-OH^2$
$=8^2-7^2$
$=15$
$O’H>0$ より $O’H=\sqrt{15}$
$AB=O’H$より $AB=\sqrt{15}$

この問題も垂線を下ろすところがポイントだね!
まとめ
● 2つの円の共通接線
[1] 互いに外部にある
共通接線4本
[2] 外接する
共通接線3本
[3] 2点で交わる
共通接線2本
[4] 内接する
共通接線1本
[5] 一方が他方の内部にある
共通接線なし
● 2つの円の共通接線に関する問題
垂線を下ろすところがポイント




コメント