高校数学Ⅱの【三角関数】で学ぶ『2倍角の公式を用いる方程式』について解説!
2倍角の公式を用いて式変形をして,三角関数に関する方程式を解く手順をまとめました!
この投稿を見れば,2倍角の公式を用いる三角関数の方程式はバッチリ!
2倍角の公式

方程式で使う「2倍角の公式」はこの3つ!
$\sin2\alpha=2\sin\alpha\cos\alpha$
$\cos2\alpha=1-2\sin^2\alpha$
$\cos2\alpha=2\cos^2\alpha-1$
「2倍角の公式」詳しくはこれ↓

余弦の2倍角の公式を用いる問題

$\cos2\alpha=1-2\sin^2\alpha$
$\cos2\alpha=2\cos^2\alpha-1$
を使い分けて問題を解いてみよう!
$\cos2\alpha=2\cos^2\alpha-1$ を用いる問題

$\cos2\alpha$ を $\cos\alpha$ に置き換えたいときは
$\cos2\alpha=2\cos^2\alpha-1$ を使おう!
$\cos2\theta-3\cos\theta+2≦0$
$(2\cos^2\theta-1)-3\cos\theta+2≦0$
$2\cos^2\theta-3\cos\theta+1≦0$
$(\cos\theta-1)(2\cos\theta-1)≦0$
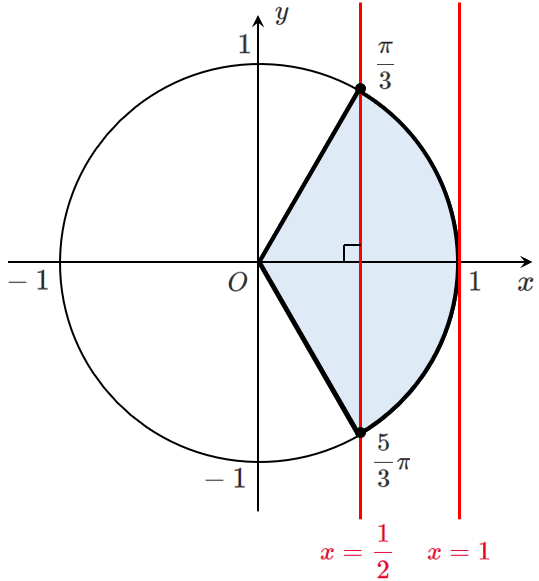
$\displaystyle{\frac{1}{2}≦\cos\theta≦1}$
$0≦\theta<2\pi$ より $\displaystyle{0≦\theta≦\frac{\pi}{3},\frac{5}{3}\pi≦\theta<2\pi}$
$\cos2\alpha=1-2\sin^2\alpha$ を用いる問題

$\cos2\alpha$ を $\sin\alpha$ に置き換えたいときは
$\cos2\alpha=1-2\sin^2\alpha$ を使おう!
$\cos2\theta-\sin\theta<0$
$(1-2\sin^2\theta)-\sin\theta<0$
$-2\sin^2\theta-\sin\theta+1<0$
$2\sin^2\theta+\sin\theta-1>0$
$(\sin\theta+1)(2\sin\theta-1)>0$
$\displaystyle{\sin\theta<-1,\frac{1}{2}<\sin\theta}$
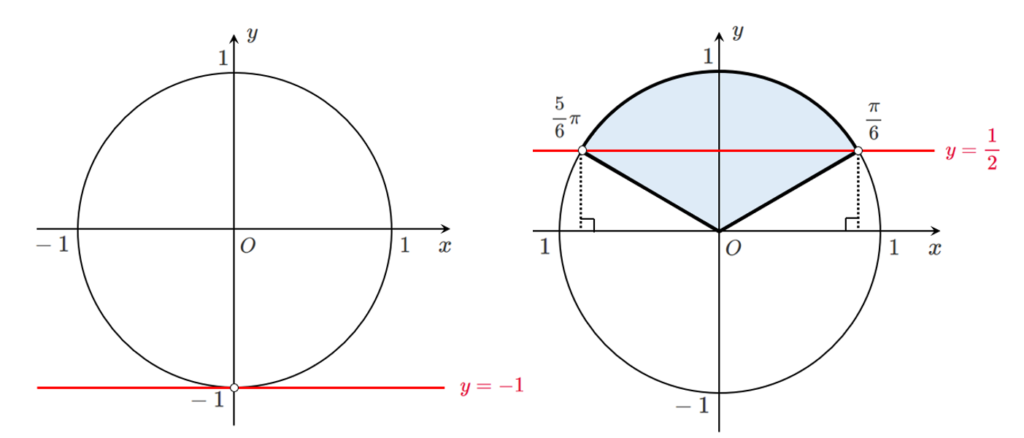
$\sin\theta<-1$ を満たす $\theta$ は存在しないので
$0≦\theta<2\pi$ より,$\displaystyle{\frac{1}{2}<\sin\theta}$ を解くと $\displaystyle{\frac{\pi}{6}<\theta<\frac{5}{6}\pi}$
【因数分解後の別解】
$(\sin\theta+1)(2\sin\theta-1)>0$
$\sin\theta+1>0$ より $2\sin\theta-1>0$
すなわち $\displaystyle{\sin\theta>\frac{1}{2}}$
$0≦\theta<2\pi$ より $\displaystyle{\frac{\pi}{6}<\theta<\frac{5}{6}\pi}$
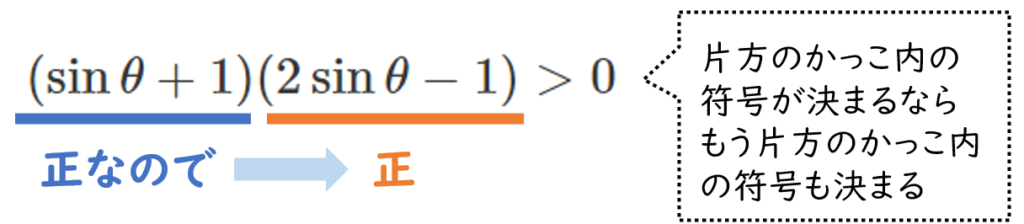
正弦の2倍角の公式を用いる方程式

$\sin2\alpha=2\sin\alpha\cos\alpha$
を使って問題を解いてみよう!
$\sin\theta$ または $\cos\theta$ だけの式にできないので,

を利用して,三角関数の不等式を解く
$\sin2\theta-\sin\theta<0$
$2\sin\theta\cos\theta-\sin\theta<0$
$\sin\theta(2\cos\theta-1)<0$
または
\begin{align} \left\{ \begin{array}{ll} \sin\theta < 0 \\ 2\cos\theta-1 > 0 \end{array} \right. \end{align}[1] $\sin\theta>0$,$\displaystyle{\cos\theta<\frac{1}{2}}$ のとき,$0≦\theta<2\pi$ の範囲で
$\sin\theta>0$ より $0<\theta<\pi$
$\displaystyle{\cos\theta<\frac{1}{2}}$ より $\displaystyle{\frac{\pi}{3}<\theta<\frac{5}{3}\pi}$
これらをともに満たす $\theta$ の範囲は $\displaystyle{\frac{\pi}{3}<\theta<\pi}$
[2] $\sin\theta<0$,$\displaystyle{\cos\theta>\frac{1}{2}}$ のとき,$0≦\theta<2\pi$ の範囲で
$\sin\theta<0$ より $\pi<\theta<2\pi$
$\displaystyle{\cos\theta>\frac{1}{2}}$ より $\displaystyle{0≦\theta<\frac{\pi}{3},\frac{5}{3}\pi<\theta<2\pi}$
これらをともに満たす $\theta$ の範囲は $\displaystyle{\frac{5}{3}\pi<\theta<2\pi}$
[1],[2] より $\displaystyle{\frac{\pi}{3}<\theta<\pi}$,$\displaystyle{\frac{5}{3}\pi<\theta<2\pi}$
【補足】
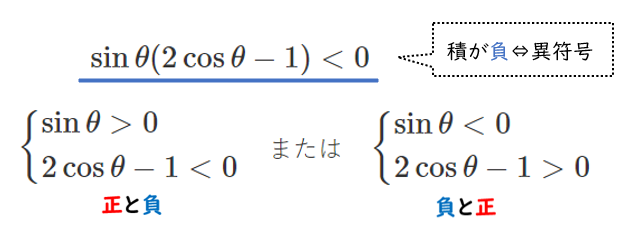




コメント