2次関数がx軸から切り取る線分の長さの求め方はわかる?
2次関数とx軸の共有点の座標が求まれば簡単に求めることができる!
知っていれば確実に解けるようになるので,
この投稿を見て解けるように練習しよう!
2次関数がx軸から切り取る線分の長さとは

2次関数が $x$ 軸から切り取る線分はこれ!
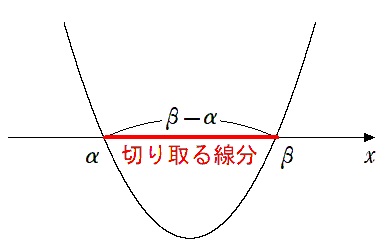
$α,β$ は2次関数と $x$ 軸の共有点の $x$ 座標
2次関数と $x$ 軸の共有点の求め方はこれ↓
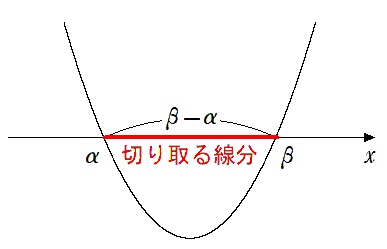
$α<β$ のとき,
2次関数が $x$ 軸から切り取る線分の長さは $β-α$
$y=0$ を代入すると
$x^2-3x+1=0$
$\displaystyle{x=\frac{3±\sqrt{5}}{2}}$
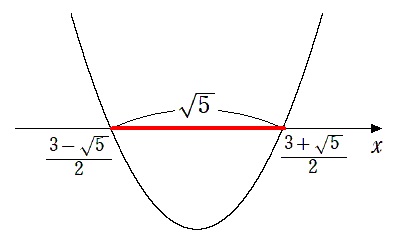
$x$ 軸との共有点は
$\displaystyle{\left(\frac{3-\sqrt{5}}{2},0\right)}$,$\displaystyle{\left(\frac{3+\sqrt{5}}{2},0\right)}$
切り取る線分の長さは
$\displaystyle{\frac{3+\sqrt{5}}{2}-\frac{3-\sqrt{5}}{2}=\sqrt{5}}$
まとめ
● 2次関数が $x$ から切り取る線分の長さ
2次関数と $x$ 軸の共有点の $x$ 座標が $α,β$ ($α<β$) のとき
2次関数が $x$ 軸から切り取る線分の長さは $β-α$
問題
問題 次の2次関数が $x$ 軸から切り取る線分の長さを求めよ。
(1) $y=3x^2-5x+1$
(2) $y=ax^2+bx+c$ $(a>0)$
解答
(1) $y=3x^2-5x+1$
$y=0$ を代入すると
$3x^2-5x+1=0$
$\displaystyle{x=\frac{5±\sqrt{13}}{6}}$
$x$ 軸との共有点は
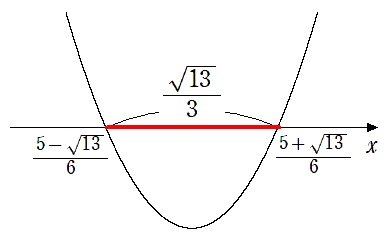
$\displaystyle{\left(\frac{5-\sqrt{13}}{6},0\right)}$,$ \displaystyle{\left (\frac{5+\sqrt{13}}{6},0\right)}$
切り取る線分の長さは
$\displaystyle{\frac{5+\sqrt{13}}{6}-\frac{5-\sqrt{13}}{6}=\frac{\sqrt{13}}{3}}$
(2) $y=ax^2+bx+c$ $(a>0)$
$y=0$ を代入すると
$ax^2+bx+c=0$
$\displaystyle{x=\frac{-b±\sqrt{b^2-4ac}}{2a}}$
$x$ 軸との共有点は
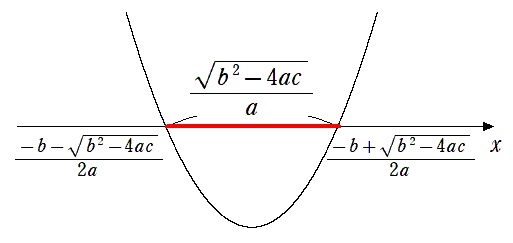
$\displaystyle{\left(\frac{-b-\sqrt{b^2-4ac}}{2a},0\right)}$,$\displaystyle{\left (\frac{-b+\sqrt{b^2-4ac}}{2a},0\right)}$
切り取る線分の長さは
$\displaystyle{\frac{-b+\sqrt{b^2-4ac}}{2a}-\frac{-b-\sqrt{b^2-4ac}}{2a}=\frac{\sqrt{b^2-4ac}}{a}}$

$D=b^2-4ac$ とすると
切り取られる線分の長さは $\displaystyle{\frac{\sqrt{D}}{a}}$ で表されるよ!
覚えて使ってもOK!
🔵2次関数のグラフの平行移動・対称移動
🔴軸に定数を含む2次関数の最大・最小の場合分け
🔴定義域の片端に定数を含む2次関数の最大・最小の場合分け
🔴定義域の両端に定数を含む2次関数の最大・最小の場合分け
🔵因数分解形の利用した2次関数の決定
🔴場合分けが必要な文字係数の方程式
🔵2次関数のグラフと係数の符号
🔵絶対不等式
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント