高校数学Ⅱの【三角関数】で学ぶ『2直線のなす角』について解説!
2直線のなす角は,$\tan\theta$ と加法定理で考えることができる!
この投稿を見れば,『2直線のなす角』に関する問題はバッチリ!
$\tan\theta$ は傾き
$\displaystyle{\tan\theta=\frac{y}{x}}$ と表されるので『傾き』を表している
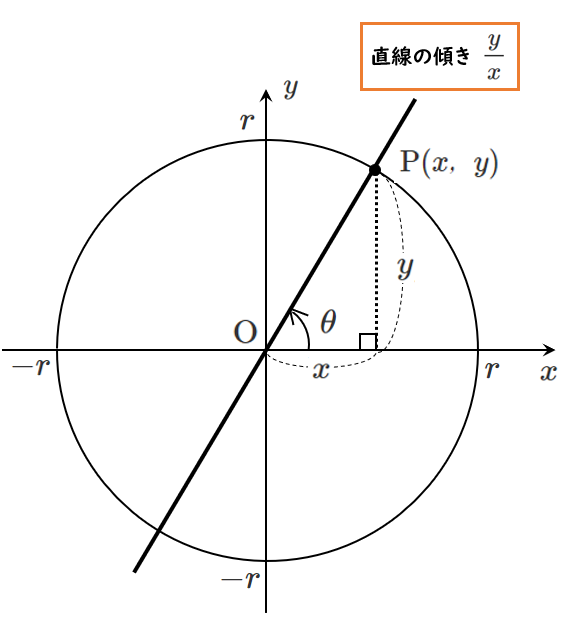
直線と $x$ 軸の正の向きとなす角を $\theta$ ($0≦\theta<\pi$) とすると
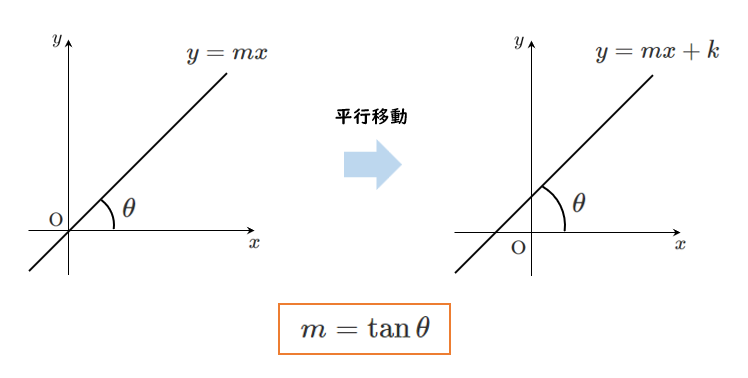
$\tan\theta$ の加法定理
$\displaystyle{\tan(\alpha+\beta)=\frac{\tan\alpha+\tan\beta}{1-\tan\alpha\tan\beta}}$
$\displaystyle{\tan(\alpha-\beta)=\frac{\tan\alpha-\tan\beta}{1+\tan\alpha\tan\beta}}$
問題
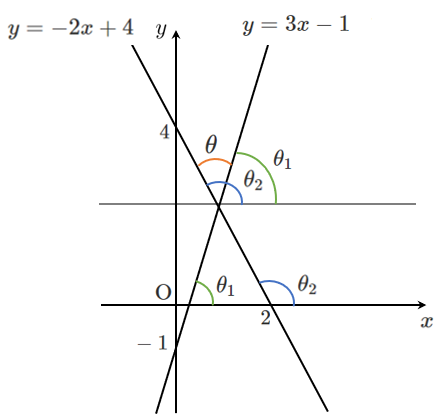
直線①は $y=3x-1$ であり,傾きは $3$
直線②は $y=-2x+4$ であり,傾きは $-2$
①,②が $x$ 軸の正の向きとなす角をそれぞれ $\theta_1$,$\theta_2$ とすると
$\tan\theta_1=3$,$\tan\theta_2=-2$
$\theta=\theta_2-\theta_1$ であるから
$\tan\theta=\tan(\theta_2-\theta_1)$
$\displaystyle{=\frac{\tan\theta_2-\tan\theta_1}{1+\tan\theta_2\tan\theta_1}}$
$\displaystyle{=\frac{-2-3}{1+(-2)\cdot3}=1}$
$\displaystyle{0≦\theta≦\frac{\pi}{2}}$ より $\displaystyle{\theta=\frac{\pi}{4}}$




コメント