
ベクトルの最重要「2直線の交点におけるベクトル」を学ぼう!
1次独立なベクトル
$\vec{a}$ と $\vec{b}$ は1次独立
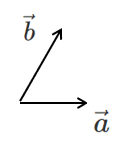
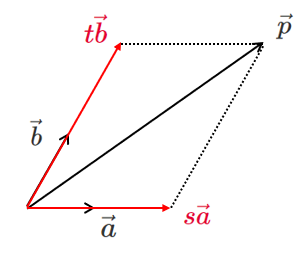
$\vec{p}=s\vec{a}+t\vec{b}$

1次独立な2つのベクトルを用いて平面上のベクトルを表したとき,表し方は1通りに定まる!
この後,使うので覚えておこう!
内分点におけるベクトル
$\triangle ABC$ において,線分 $AB$ を $m:n$ に内分する点を $P$ とするとき
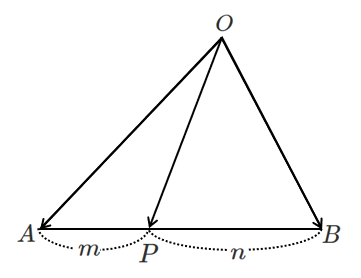
$\displaystyle{\overrightarrow{OP}=\frac{n\overrightarrow{OA}+m\overrightarrow{OB}}{m+n}}$
「内分点におけるベクトル」詳しくはこれ↓

2直線の交点におけるベクトル①
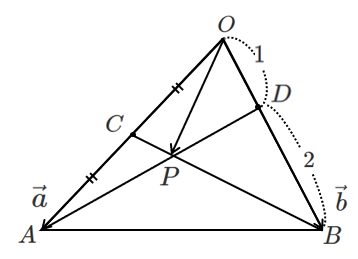

どうやって解けばいいのかな?

問題の考え方を整理しておこう!
$P$ は線分 $AD$ の内分点なので,$AP:PD$ の比をおいて $\overrightarrow{OP}$ を表す
$P$ は線分 $BC$ の内分点なので,$BP:PC$ の比をおいて $\overrightarrow{OP}$ を表す
$\overrightarrow{OP}$ の表し方は1通りなので,$\vec{a}$ と $\vec{b}$ の係数を比較する

$\overrightarrow{OP}$ を2通りで表して係数比較!

解き方は分かったけど,比のおき方はどうやっておくの?

比のおき方もコツがあるよ!
例えば
$\triangle ABC$ について,線分 $AB$ 上に点 $P$ があるとき
$AP:PB=s:(1-s)$ とおくと($s$ は実数)
\begin{eqnarray} \overrightarrow{OP} &=& \frac{(1-s)\overrightarrow{OA}+s\overrightarrow{OB}}{s+(1-s)} \\\\ &=& (1-s)\overrightarrow{OA}+s\overrightarrow{OB} \end{eqnarray}
和が1になるように比をおくことで,分母が1になるから分数にならないね!

その通り!
計算が楽になるんだ!
じゃあ問題を解いてみよう!

点 $C$ は辺 $OA$ の中点なので
$\displaystyle{\overrightarrow{OC}=\frac{1}{2}\vec{a}}$
点 $D$ は辺 $OB$ を $1:2$ に内分する点なので
$\displaystyle{\overrightarrow{OD}=\frac{1}{3}\vec{b}}$
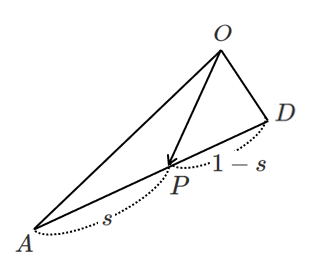
$AP:PD=s:(1-s)$ とすると ($s$ は実数)
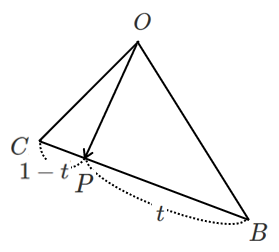
$BP:PC=t:(1-t)$ とすると ($t$ は実数)
$\vec{a}$,$\vec{b}$ は一次独立なので,$\overrightarrow{OP}$ の表し方は1通りに定まる
①と②より,$\vec{a}$ と $\vec{b}$ の係数を比較して
\begin{cases} 1-s=\frac{1}{2}t \\\\ \frac{1}{3}s=1-t \end{cases}これを解いて
$\displaystyle{s=\frac{3}{5}}$,$\displaystyle{t=\frac{4}{5}}$
①または②に代入して
$\displaystyle{\overrightarrow{OP}=\frac{2}{5}\vec{a}+\frac{1}{5}\vec{b}}$
2直線の交点におけるベクトル②
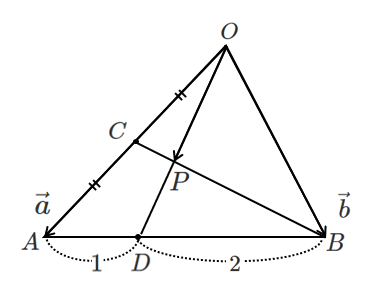

この問題も,$\overrightarrow{OP}$ を2通りで表して係数比較!

1つは$BP:PC$ を比でおくのは分かるけど,もう1つはどうするの?

$O$,$P$,$D$ が一直線上に並ぶので,$\overrightarrow{OP}=k\overrightarrow{OD}$ という式を使おう!
$P$ は線分 $BC$ の内分点なので,$BP:PC$ の比をおいて $\overrightarrow{OP}$ を表す
$P$ は線分 $OD$ 上の点なので,$\overrightarrow{OP}=k\overrightarrow{OD}$ とおいて $\overrightarrow{OP}$ を表す
$\overrightarrow{OP}$ の表し方は1通りなので,$\vec{a}$ と $\vec{b}$ の係数を比較する
点 $C$ は辺 $OA$ の中点なので
$\displaystyle{\overrightarrow{OC}=\frac{1}{2}\vec{a}}$
点 $D$ は辺 $AB$ を $1:2$ に内分する点なので
\begin{eqnarray} \overrightarrow{OD} &=& \frac{2\overrightarrow{OA}+\overrightarrow{OB}}{1+2} \\\\ &=& \frac{2}{3}\vec{a}+\frac{1}{3}\vec{b} \\\\ \end{eqnarray}$BP:PC=t:(1-t)$ とすると ($t$ は実数)

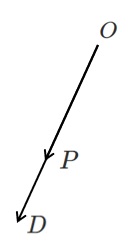
点 $P$ は線分 $OD$ 上にあるので
$\overrightarrow{OP}=k\overrightarrow{OD}$ とすると($k$ は実数)
$\vec{a}$,$\vec{b}$ は一次独立なので,$\overrightarrow{OP}$ の表し方は1通りに定まる
①と②より,$\vec{a}$ と $\vec{b}$ の係数を比較して
\begin{cases} \frac{1}{2}t=\frac{2}{3}k \\\\ 1-t=\frac{1}{3}k \end{cases}これを解いて
$\displaystyle{t=\frac{4}{5}}$,$\displaystyle{k=\frac{3}{5}}$
①または②に代入して
$\displaystyle{\overrightarrow{OP}=\frac{2}{5}\vec{a}+\frac{1}{5}\vec{b}}$
まとめ
● 1次独立なベクトル
$0$ ではない2つのベクトル $\vec{a}$,$\vec{b}$ が平行でないとき,$\vec{a}$ と $\vec{b}$ は1次独立という
● 平面上のベクトル
1次独立な2つのベクトルを用いて平面上のベクトルを表したとき,表し方は1通りに定まる
● 2直線の交点におけるベクトル
ベクトルを2通りで表して係数比較
表し方は ①比をおく ②定数倍($k$ 倍) を用いる

2直線の交点におけるベクトルに関する問題は最重要!
必ずマスターしよう!




コメント