高校数学Ⅱで学ぶ『3次方程式の解法と解の分類』について解説!
因数定理を用いることで3次方程式を解くことができます!
3次方程式の解の分類についても分かりやすく解説しました!
この投稿を見れば、3次方程式はバッチリ!
因数定理

高次方程式を解くときは,因数分解が必要不可欠!
「因数定理」による因数分解をおさえておこう!
因数定理の復習はこれ↓
3次方程式の解の分類
3次方程式を解く場合は、因数定理を利用することが多いです。
因数分解の公式
$a^3\pm3a^2b+3ab^2\pm b^3=(a\pm b)^3$
$a^3\pm b^3=(a\pm b)(a^2\mp ab+b^2)$
が利用できることもあります。
3次方程式の因数分解と解の種類は以下の通りです。
(1次式)(1次式)(1次式)=0
$P(x)=x^3-6x^2+11x-6$ とすると $P(1)=1^3-6\cdot1^2+11\cdot1-6=0$
$P(1)=0$ より,$P(x)$ は $x-1$ を因数にもつ
すなわち,$x^3-6x^2+11x-6$ は $x-1$ を因数にもつ
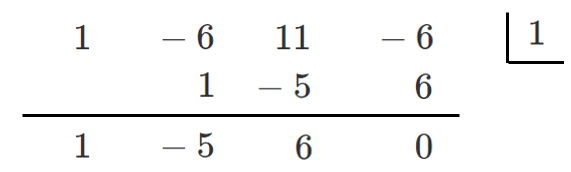
以上より, $x^3-6x^2+11x-6=(x-1)(x^2-5x+6)$
$x^3-6x^2+11x-6=0$
$(x-1)(x^2-5x+6)=0$
$(x-1)(x-2)(x-3)=0$
$x=1,2,3$ 異なる3つの実数解
(1次式)(1次式)²=0
$P(x)=x^3-x^2-8x+12$ とすると $P(2)=2^3-2^2-8\cdot2+12=0$
$P(2)=0$ より,$P(x)$ は $x-2$ を因数にもつ
すなわち,$x^3-x^2-8x+12$ は $x-2$ を因数にもつ
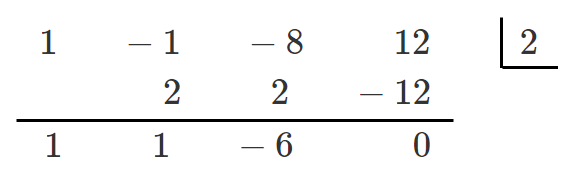
以上より, $x^3-x^2-8x+12=(x-2)(x^2+x-6)$
$x^3-x^2-8x+12=0$
$(x-2)(x^2+x-6)=0$
$(x-2)(x-2)(x+3)=0$
$(x-2)^2(x+3)=0$
$x=2,-3$ 異なる2つの実数解($x=2$ は $2$ 重解)
$( )^2=0$ から求まる解を $2$ 重解という
(1次式)³=0
$P(x)=x^3-3x^2+3x-1$ とすると $P(1)=1^3-3\cdot1^2+3\cdot1-1=0$
$P(1)=0$ より,$P(x)$ は $x-1$ を因数にもつ
すなわち,$x^3-3x^2+3x-1$ は $x-1$ を因数にもつ
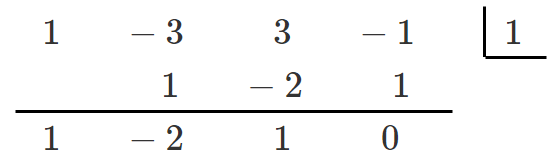
以上より, $x^3-3x^2+3x-1=(x-1)(x^2-2x+1)$
$x^3-3x^2+3x-1=0$
$(x-1)(x^2-2x+1)=0$
$(x-1)(x-1)^2=0$
$(x-1)^3=0$
$x=1$ 1つの実数解($3$ 重解)
$( )^3=0$ から求まる解を $3$ 重解という
【別解】因数分解の公式を用いて解くことができる
$a^3-3a^2b+3ab^2-b^3=(a-b)^3$ より,
$x^3-3x^2+3x-1=(x-1)^3$
よって, $x^3-3x^2+3x-1=0$
$(x-1)^3=0$
$x=1$
(1次式)(2次式)=0
(1) $x^3-4x^2+4x-1=0$
(2) $x^3-2x^2+2x-1=0$
(1) $x^3-4x^2+4x-1=0$
$P(x)=x^3-4x^2+4x-1$ とすると $P(1)=1^3-4\cdot1^2+4\cdot1-1=0$
$P(1)=0$ より,$P(x)$ は $x-1$ を因数にもつ
すなわち,$x^3-4x^2+4x-1$ は $x-1$ を因数にもつ
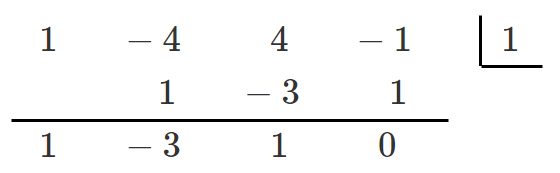
以上より, $x^3-4x^2+4x-1=(x-1)(x^2-3x+1)$
$x^3-4x^2+4x-1=0$
$(x-1)(x^2-3x+1)=0$
$x-1=0$ または $x^2-3x+1=0$
$\displaystyle{x=1,\frac{3±\sqrt{5}}{2}}$ 異なる3つの実数解
(2) $x^3-2x^2+2x-1=0$
$P(x)=x^3-2x^2+2x-1$ とすると $P(1)=1^3-2\cdot1^2+2\cdot1-1=0$
$P(1)=0$ より,$P(x)$ は $x-1$ を因数にもつ
すなわち,$x^3-2x^2+2x-1$ は $x-1$ を因数にもつ
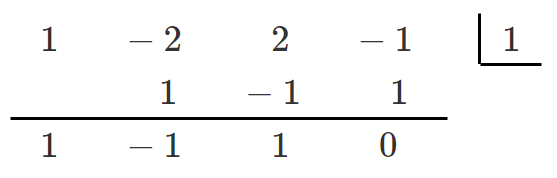
以上より, $x^3-2x^2+2x-1=(x-1)(x^2-x+1)$
$x^3-2x^2+2x-1=0$
$(x-1)(x^2-x+1)=0$
$x-1=0$ または $x^2-x+1=0$
$\displaystyle{x=1,\frac{1±\sqrt{3}i}{2}}$ 1つの実数解と異なる2つの虚数解
まとめ
● 3次方程式の解き方
「因数定理」を用いて因数分解して解く
「因数分解の公式」を用いて解ける場合もある
● 3次方程式の因数分解と解の種類
(1次式)(1次式)(1次式)=0 … 異なる3つの実数解
(1次式)(1次式)²=0 … 異なる2つの実数解(片方は $2$ 重解)
(1次式)³=0 … 1つの実数解( $3$ 重解)
(1次式)(2次式)=0 … 異なる3つの実数解 または 1つの実数解と異なる2つの虚数解

解けるようになるまで練習あるのみ!




コメント