高校数学Ⅱで学ぶ『3次方程式の解の判別』に関する応用問題の解説です!
「3次方程式が重解をもつ」
「3次方程式が異なる3つの実数解をもつ」
「3次方程式が虚数解をもつ」
といった問題についてわかりやすく解説しました!
問題
(1) 重解
(2) 異なる3つの実数解
(3) 虚数解
因数定理を利用して因数分解
3次方程式は、まずは (1次式)(2次式)=0 の形に因数分解する

$P(x)=x^3-(a-1)x^2+(a+2)x-4$ とすると
$P(1)=0$ より,$P(x)$ は $x-1$ を因数にもつ ← 因数定理
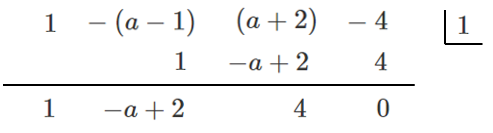
よって $(x-1)\{x^2-(a-2)x+4\}=0$
$x=1$ または $x^2-(a-2)x+4=0$

2次方程式 $x^2-(a-2)x+4=0$ がどのような解をもてばよいかを考える
3次方程式が重解をもつ

$x^3-(a-1)x^2+(a+2)x-4=0$
$(x-1)\{x^2-(a-2)x+4\}=0$
$x=1$ または $x^2-(a-2)x+4=0$ … ①
①の判別式を $D$ とすると
$D=(a-2)^2-4\cdot4=a^2-4a-12=(a+2)(a-6)$
$D=0$ のとき $a=-2,6$
$a=-2$ のとき①は $x^2+4x+4=0$ すなわち $(x+2)^2=0$
重解は $x=-2$
$a=6$ のとき①は $x^2-4x+4=0$ すなわち $(x-2)^2=0$
重解は $x=2$
ここをタッチ!
2次方程式 $ax^2+bx+c=0$ の重解は $\displaystyle{x=-\frac{b}{2a}}$ なので
①が重解をもつとき,その重解は $\displaystyle{x=\frac{a-2}{2}}$
$a=-2$ のときの重解は $x=-2$
$a=6$ のときの重解は $x=2$
よって $a=-2,6$
[2] ①が $x=1$ の解をもつとき
$x=1$ を①に代入して $1^2-(a-2)\cdot1+4=0$
これを解いて $a=7$
$a=7$ のとき $x^2-5x+4=0$ すなわち $(x-1)(x-4)=0$
①は $x=1$ を解にもつ
[1],[2] より $a=-2,6,7$
$a=6$ のとき,3次方程式は $(x-1)(x-2)^2=0$ より $x-1$,$x=2$(重解)
$a=7$ のとき,3次方程式は $(x-1)^2(x-4)=0$ より $x=1$(重解),$x=4$
3次方程式が異なる3つの実数解をもつ

$x^3-(a-1)x^2+(a+2)x-4=0$
$(x-1)\{x^2-(a-2)x+4\}=0$
$x=1$ または $x^2-(a-2)x+4=0$ … ①
①が $x=1$ 以外の異なる2つの実数解をもつことが条件である
①の判別式を $D$ とすると
$D=(a-2)^2-4\cdot4=a^2-4a-12=(a+2)(a-6)$
$D>0$ より $a<-2$,$6<a$ … ②
①に $x=1$ を代入すると $1^2-(a-2)\cdot1+4=0$
これを解いて $a=7$
$a=7$ のとき①は $x=1$ を解にもつので $a≠7$ … ③
②,③より $a<-2$,$6<a<7$,$7<a$
3次方程式が虚数解をもつ

$x^3-(a-1)x^2+(a+2)x-4=0$
$(x-1)\{x^2-(a-2)x+4\}=0$
$x=1$ または $x^2-(a-2)x+4=0$ … ①
①が虚数解をもつことが条件である
①の判別式を $D$ とすると
$D=(a-2)^2-4\cdot4=a^2-4a-12=(a+2)(a-6)$
$D<0$ より $-2<a<6$




コメント