高校数学Ⅱで学ぶ『4次方程式の解法』をわかりやすく解説!
4次方程式を解くために、4種類のパターンを理解する必要があります!
この投稿を見れば、4次方程式の問題はバッチリ!
4次方程式のパターン
4次方程式は以下のパターンを知っておきましょう。
因数定理
4次方程式も3次方程式と同様に因数定理を利用して解くことができる。
$P(x)=2x^4-3x^3+7x^2+7x-5$ とすると
$P(-1)=0$ より,$P(x)$ は $x+1$ を因数にもつ
$P(x)=(x+1)(2x^3-5x^2+12x-5)$
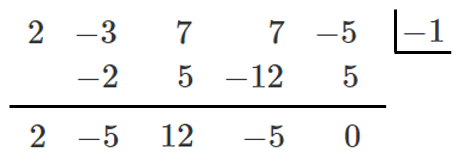
$Q(x)=2x^3-5x^2+12x-5$ とすると
$\displaystyle{Q\left(\frac{1}{2}\right)=0}$ より,$Q(x)$ は $\displaystyle{x-\frac{1}{2}}$ を因数にもつ
$\displaystyle{Q(x)=\left(x-\frac{1}{2}\right)(2x^2-4x+10)}$
$=(2x-1)(x^2-2x+5)$
よって $P(x)=(x+1)(2x-1)(x^2-2x+5)$
$P(x)=0$ より $(x+1)(2x-1)(x^2-2x+5)=0$
$x+1=$ または $2x-1=0$ または $x^2-2x+5=0$
したがって $\displaystyle{x=1,\frac{1}{2},1\pm2i}$
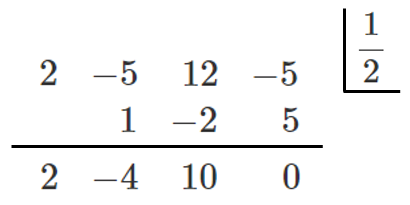
複2次式
$ax^4+bx^2+c$ のように、各項の次数が偶数の4次式を複2次式という。
② 2乗の差の形 $(○)^2-(□)^2=0$ をつくり $(○+□)(○-□)=0$ と因数分解する
(1) $x^4-2x^2-3=0$
(2) $x^4+x^2+1=0$
(3) $x^4+4=0$
(1) $x^4-2x^2-3=0$
$(x^2-3)(x^2+1)=0$
$x^2-3=0$ または $x^2+1=0$
したがって $x=\pm\sqrt{3},\pm i$
【補足】
$x^2=X$ とおくと
$X^2-2X-3=0$
$(X-3)(X+1)=0$
(2) $x^4+x^2+1=0$
$(x^4+2x^2+1)-x^2=0$
$(x^2+1)^2-x^2=0$
$\{(x^2+1)+x\}\{(x^2+1)-x\}=0$
$(x^2+x+1)(x^2-x+1)=0$
$x^2+x+1=0$ または $x^2-x+1=0$
$x^2+x+1=0$ より $\displaystyle{x=\frac{-1\pm\sqrt{3}i}{2}}$
$x^2-x+1=0$ より $\displaystyle{x=\frac{1\pm\sqrt{3}i}{2}}$
よって $\displaystyle{x=\frac{-1\pm\sqrt{3}i}{2},\frac{1\pm\sqrt{3}i}{2}}$
【補足】
$x^2$ を足して、引く
➡ $(○)^2-(□)^2$ の形
➡ $(○+□)(○-□)$ に変形
(3) $x^4+4=0$
$(x^4+4x^2+4)-4x^2=0$
$(x^2+2)^2-(2x)^2=0$
$\{(x^2+2)+2x\}\{(x^2+2)-2x\}=0$
$(x^2+2x+2)(x^2-2x+2)=0$
$x^2+2x+2=0$ または $x^2-2x+2=0$
$x^2+2x+2=$ より $x=-1\pm i$
$x^2-2x+2=$ より $x=1\pm i$
よって $x=-1\pm i,1\pm i$
【補足】
$4x^2$ を足して、引く
➡ $(○)^2-(□)^2$ の形
➡ $(○+□)(○-□)$ に変形
(3) $x^2=X$ とおくと $X^2+4=0$ となり因数分解できない
よって $( )^2-( )^2=0$ の形ができるように式変形をする
組み合わせを考える因数分解
組み合わせを工夫して因数分解することで4次方程式を解くことができる。
$(x+1)(x+2)(x+3)(x+4)=3$
$\{(x+1)(x+4)\}\{(x+2)(x+3)\}-3=0$
$(x^2+5x+4)(x^2+5x+6)-3=0$
$(x^2+5x)^2+10(x^2+5x)+24-3=0$
$(x^2+5x)^2+10(x^2+5x)+21=0$
$\{(x^2+5x)+3\}\{(x^2+5x)+7\}=0$
$(x^2+5x+3)(x^2+5x+7)=0$
$x^2+5x+3=0$ または $x^2+5x+7=0$
$x^2+5x+3=0$ より $\displaystyle{x=\frac{-5\pm\sqrt{13}}{2}}$
$x^2+5x+7=0$ より $\displaystyle{x=\frac{-5\pm\sqrt{3}i}{2}}$
よって $\displaystyle{x=\frac{-5\pm\sqrt{13}}{2},\frac{-5\pm\sqrt{3}i}{2}}$
【補足】
組み合わせを考える
➡ $x^2+5x$ が共通
$x^2+5x=A$ とおくと
$(A+4)(A+6)-3=0$
$A^2+10A+24-3=0$
$A^2+10A+21=0$
$(A+3)(A+7)=0$
相反方程式
係数が左右対称である方程式を相反方程式という。

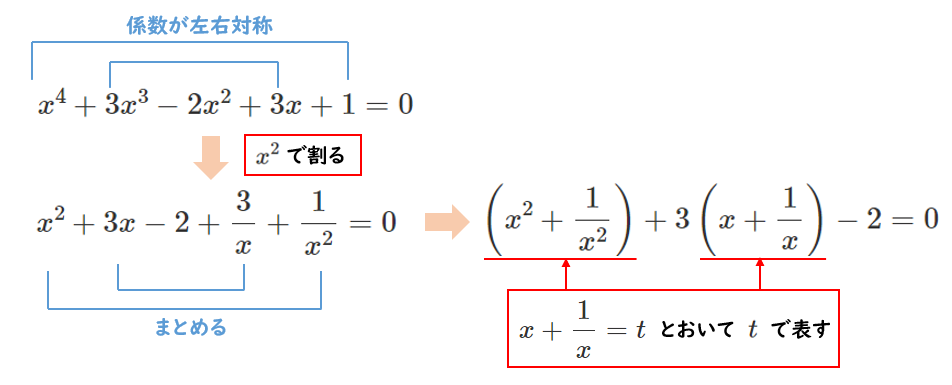
ここをタッチ!
$\displaystyle{x^2+3x-2+\frac{3}{x}+\frac{1}{x^2}=0}$
$\displaystyle{\left(x^2+\frac{1}{x^2}\right)+3\left(x+\frac{1}{x}\right)-2=0}$
$\displaystyle{\left(x+\frac{1}{x}\right)^2-2+3\left(x+\frac{1}{x}\right)-2=0}$
ここをタッチ!
$\displaystyle{=\left(x+\frac{1}{x}\right)^2-2\cdot x\cdot\frac{1}{x}}$
$\displaystyle{\left(x+\frac{1}{x}\right)^2+3\left(x+\frac{1}{x}\right)-4=0}$
$\displaystyle{x+\frac{1}{x}=t}$ とおくと
$t^2+3t-4=0$
$(t+4)(t-1)=0$
$t=-4,1$
$\displaystyle{x+\frac{1}{x}=-4}$ のとき $x^2+4x+1=0$
$x=-2\pm\sqrt{3}$
$\displaystyle{x+\frac{1}{x}=1}$ のとき $x^2-x+1=0$
$\displaystyle{x=\frac{1\pm\sqrt{3}i}{2}}$
したがって $\displaystyle{x=-2\pm\sqrt{3},\frac{1\pm\sqrt{3}i}{2}}$




コメント