
2021年度共通テスト数学ⅡBの第2問「微分法・積分法」の問題の解説!
解いたことがない人は解いてみよう!
第2問「微分法・積分法」の問題
第2問
[1] 座標平面上で,次の二つの $2$ 次関数のグラフについて考える。
$y=3x^2+2x+3$ $\cdots\cdots$ (A)
$y=2x^2+2x+3$ $\cdots\cdots$ (B)
(A),(B) の $2$ 次関数のグラフには次の共通点がある。
次の ⓪~⑤ の $2$ 次関数のグラフのうち,$y$ 軸との交点における接線の方程式が $y=\boxed{\mathbf{ イ }}x+\boxed{\mathbf{ ウ }}$ となるものは $\boxed{\mathbf{ エ }}$ である。
$\boxed{\mathbf{ エ }}$ の解答群
$a$,$b$,$c$ を $0$ でない実数とする。
曲線 $y=ax^2+bx+c$ 上の点 $(0,\boxed{\mathbf{ オ }})$ における接線を $l$ とすると,その方程式は $y=\boxed{\mathbf{ カ }}x+\boxed{\mathbf{ キ }}$ である。
接線 $l$ と $x$ 軸との交点の $x$ 座標は $\displaystyle{\frac{\boxed{\mathbf{ クケ }}}{\boxed{\mathbf{ コ }}}}$ である。
$a$,$b$,$c$ が正の実数であるとき,曲線 $y=ax^2+bx+c$ と接線 $l$ および直線 $\displaystyle{x=\frac{\boxed{\mathbf{ クケ }}}{\boxed{\mathbf{ コ }}}}$ で囲まれた図形の面積を $S$ とすると
$\displaystyle{S=\frac{ac^{\boxed{\mathbf{サ}}}}{\boxed{\mathbf{ シ }}b^{\boxed{\mathbf{ス}}}}}$ $\cdots\cdots$ (C)
である。
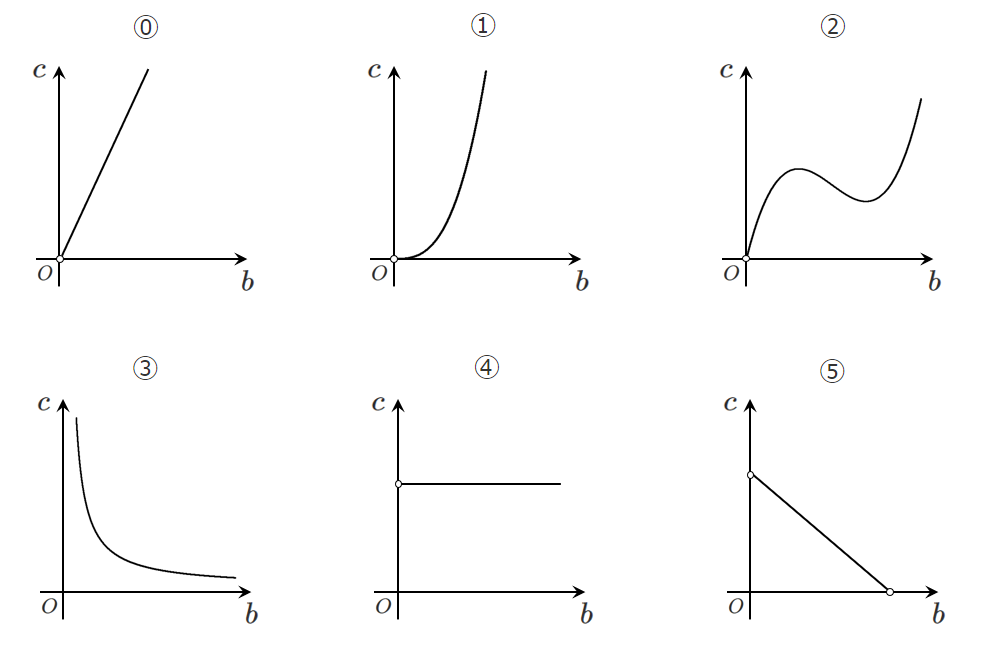
(C) において,$a=1$ とし,$S$ の値が一定となるように正の実数 $b$,$c$ の値を変化させる。このとき,$b$ と $c$ の関数を表すグラフの概形は $\boxed{\mathbf{ セ }}$ である。
$\boxed{\mathbf{ セ }}$ については,最も適当なものを,次の ⓪~⑤ のうちから一つ選べ。
(2) 座標平面上で,次の三つの $3$ 次関数のグラフについて考える。
$y=4x^3+2x^2+3x+5$ $\cdots\cdots$ (D)
$y=-2x^3+7x^2+3x+5$ $\cdots\cdots$ (E)
$y=5x^3-x^2+3x+5$ $\cdots\cdots$ (F)
(D),(E),(F) の $3$ 次関数のグラフには次の共通点がある。
$a$,$b$,$c$,$d$ を $0$ でない実数とする。
曲線 $y=ax^3+bx^2+cx+d$ 上の点 $(0,\boxed{\mathbf{ ツ }})$ における接線の方程式は $y=\boxed{\mathbf{ テ }}x+\boxed{\mathbf{ ト }}$ である。
次に,$f(x)=ax^3+bx^2+cx+d$,$g(x)=\boxed{\mathbf{ テ }}x+\boxed{\mathbf{ ト }}$ とし,$f(x)-g(x)$ について考える。
$h(x)=f(x)-g(x)$ とおく。$a$,$b$,$c$,$d$ が正の実数であるとき,$y=h(x)$ のグラフの概形は $\boxed{\mathbf{ テ }}$ である。
$y=f(x)$ のグラフと $y=g(x)$ のグラフの共有点の $x$ 座標は $\displaystyle{\frac{\boxed{\mathbf{ ニヌ }}}{\boxed{\mathbf{ ネ }}}}$ と $\boxed{\mathbf{ ノ }}$ である。また,$x$ が $\displaystyle{\frac{\boxed{\mathbf{ ニヌ }}}{\boxed{\mathbf{ ネ }}}}$ と $\boxed{\mathbf{ ノ }}$ の間を動くとき,$|f(x)-g(x)|$ の値が最大となるのは,$\displaystyle{x=\frac{\boxed{\mathbf{ ハヒフ }}}{\boxed{\mathbf{ ヘホ }}}}$ のときである。
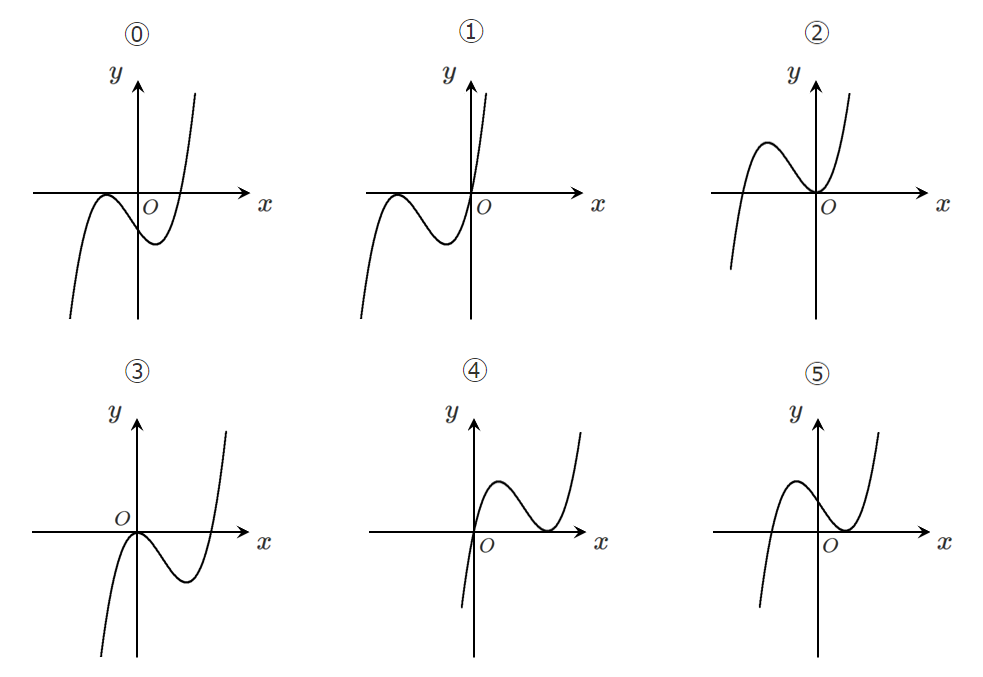
$\boxed{\mathbf{ ナ }}$ については,最も適当なものを,次の ⓪~⑤ のうちから一つ選べ。
第2問「微分法・積分法」の分析と対策

この問題を分析するとこんな感じかな!
問題で扱われている分野と力

間違えた問題を分析すれば,自分がどこでつまずいているか分かるよ!
- $y$ 軸との交点の座標 $\boxed{\mathbf{ア}}$,$\boxed{\mathbf{オ}}$,$\boxed{\mathbf{ク}}~\boxed{\mathbf{コ}}$,$\boxed{\mathbf{ソ}}$,$\boxed{\mathbf{ツ}}$
- 接点が与えられている場合の接線の方程式 $\boxed{\mathbf{イ}}~\boxed{\mathbf{エ}}$,$\boxed{\mathbf{カ}},\boxed{\mathbf{キ}}$,$\boxed{\mathbf{タ}},\boxed{\mathbf{チ}}$,$\boxed{\mathbf{テ}},\boxed{\mathbf{ト}}$
- 2曲線の間の面積 $\boxed{\mathbf{サ}}~\boxed{\mathbf{ス}}$
- 比例関係 $\boxed{\mathbf{セ}}$
- 3次関数のグラフ $\boxed{\mathbf{ナ}}$
- 2曲線の共有点の座標 $\boxed{\mathbf{ニ}}~\boxed{\mathbf{ネ}}$
- 絶対値と3次関数の最大値 $\boxed{\mathbf{ハ}}~\boxed{\mathbf{ホ}}$
問題の分析
$y$ 軸との交点と接線の方程式が何度も問われる
接線の方程式を求めることが苦手な受験生は苦戦した問題
接線の方程式は出題される可能性が高いので,求められるようにしておこう
ちなみに,接線の方程式の問題には
- 接点が与えられている場合 ←今回はこっち
- 接点が与えられていない場合
の2パターンを解けるようにしておく必要がある
$y=ax^3+bx^2+cx+d$ など,一般化した関数を扱う問題なので文字が多い
$y=2x^3+3x^2+x-1$ のような数で表される関数と同様に考えればよいが,
文字になると難しいと感じる受験生は苦戦した
対策
微分と積分は出題されるテーマが限られる
- 接線の方程式
- 3次関数のグラフと極値
- 曲線で囲まれる面積
これらのテーマの問題をしっかり練習しよう
第2問「微分法・積分法」の解答
(1)
第2問
[1] 座標平面上で,次の二つの $2$ 次関数のグラフについて考える。
$y=3x^2+2x+3$ $\cdots\cdots$ (A)
$y=2x^2+2x+3$ $\cdots\cdots$ (B)
(A),(B) の $2$ 次関数のグラフには次の共通点がある。
次の ⓪~⑤ の $2$ 次関数のグラフのうち,$y$ 軸との交点における接線の方程式が $y=\boxed{\mathbf{ イ }}x+\boxed{\mathbf{ ウ }}$ となるものは $\boxed{\mathbf{ エ }}$ である。
$\boxed{\mathbf{ エ }}$ の解答群
$a$,$b$,$c$ を $0$ でない実数とする。
曲線 $y=ax^2+bx+c$ 上の点 $(0,\boxed{\mathbf{ オ }})$ における接線を $l$ とすると,その方程式は $y=\boxed{\mathbf{ カ }}x+\boxed{\mathbf{ キ }}$ である。
接線 $l$ と $x$ 軸との交点の $x$ 座標は $\displaystyle{\frac{\boxed{\mathbf{ クケ }}}{\boxed{\mathbf{ コ }}}}$ である。
$a$,$b$,$c$ が正の実数であるとき,曲線 $y=ax^2+bx+c$ と接線 $l$ および直線 $\displaystyle{x=\frac{\boxed{\mathbf{ クケ }}}{\boxed{\mathbf{ コ }}}}$ で囲まれた図形の面積を $S$ とすると
$\displaystyle{S=\frac{ac^{\boxed{\mathbf{サ}}}}{\boxed{\mathbf{ シ }}b^{\boxed{\mathbf{ス}}}}}$ $\cdots\cdots$ (C)
である。
(C) において,$a=1$ とし,$S$ の値が一定となるように正の実数 $b$,$c$ の値を変化させる。このとき,$b$ と $c$ の関数を表すグラフの概形は $\boxed{\mathbf{ セ }}$ である。
$\boxed{\mathbf{ セ }}$ については,最も適当なものを,次の ⓪~⑤ のうちから一つ選べ。

$y=3x^2+2x+3$ $\cdots\cdots$ (A)
$y=2x^2+2x+3$ $\cdots\cdots$ (B)
(A) も (B) も $x=0$ を代入したら,$y=3$ となる
よって,$y$ 軸との交点の $y$ 座標は $\boxed{\mathbf{3}}$ である
(A) について微分すると $y’=6x+2$
(B) について微分すると $y’=4x+2$
どちらも $x=0$ における微分係数は $2$ となる
すなわち,$x=0$ における接線の傾きが $2$
接線は傾き $2$,$(0,3)$ を通るので,$y=\boxed{\mathbf{2}}x+\boxed{\mathbf{3}}$
$x=a$ における微分係数とは,微分して $x=a$ を代入した値のこと

接線を求めるだけなら,図を描かずに式だけで求められるようにしよう!
接線の方程式についてはこれ↓

$y$ 軸との交点における接線の方程式は $y=\boxed{\mathbf{2}}x+\boxed{\mathbf{3}}$ のとき,これは $(0,3)$ を通る
よって,選択肢の中で $(0,3)$ を通る $2$ 次関数は④または⑤
$x=0$ における微分係数(接線の傾き)が $2$ になる方が答えになる
④は $y’=-2x+2$ より,$x=0$ における微分係数が $2$
⑤は $y’=-2x-2$ より,$x=0$ における微分係数が $-2$
したがって,$\boxed{\mathbf{④}}$
曲線 $y=ax^2+bx+c$ 上の点 $(0,\boxed{\mathbf{c}})$ における接線 $l$ について
$y’=2ax+b$ より,$x=0$ における微分係数(接線の傾き)は $b$
よって,接線 $l$ の方程式は $y=\boxed{\mathbf{b}}x+\boxed{\mathbf{c}}$ である
接線 $l$ と $x$ 軸の交点は $y=0$ を代入して
$bx+c=0$
$\displaystyle{x=\frac{\boxed{\mathbf{-c}}}{\boxed{\mathbf{b}}}}$
$a$,$b$,$c$ が正の実数であるとき,
曲線 $y=ax^2+bx+c$ と接線 $l$ および直線 $\displaystyle{x=\frac{\boxed{\mathbf{-c}}}{\boxed{\mathbf{b}}}}$ で囲まれた図形の面積 $S$ は
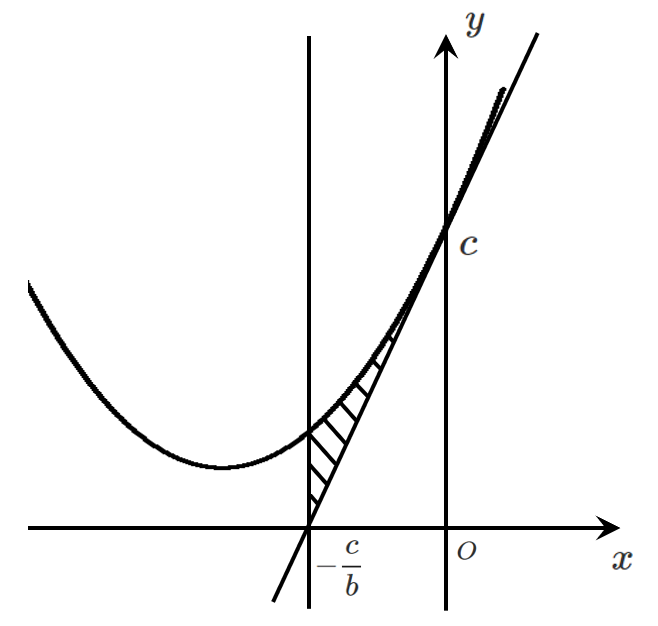
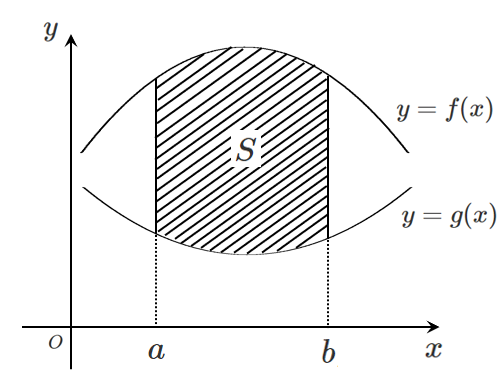
$f(x)$ が $g(x)$ より上側にあるとき $\displaystyle{S=\int_a^b \left\{f(x)-g(x)\right\} dx}$
2曲線の間の面積の求め方はこれ↓
$a=1$ のとき, $\displaystyle{S=\frac{1}{3}\left(\frac{c}{b}\right)^3}$
$S$ が定数となるとき,$\displaystyle{\frac{c}{b}}$ も定数となる
$b>0$,$c>0$ なので,$k>0$ を満たす定数 $k$ を用いると
$\displaystyle{\frac{c}{b}=k}$
すなわち, $c=kb$ と表される
$b$ と $c$ は比例の関係にあるので,$\boxed{\mathbf{⓪}}$
(2)
(2) 座標平面上で,次の三つの $3$ 次関数のグラフについて考える。
$y=4x^3+2x^2+3x+5$ $\cdots\cdots$ (D)
$y=-2x^3+7x^2+3x+5$ $\cdots\cdots$ (E)
$y=5x^3-x^2+3x+5$ $\cdots\cdots$ (F)
(D),(E),(F) の $3$ 次関数のグラフには次の共通点がある。
$a$,$b$,$c$,$d$ を $0$ でない実数とする。
曲線 $y=ax^3+bx^2+cx+d$ 上の点 $(0,\boxed{\mathbf{ ツ }})$ における接線の方程式は $y=\boxed{\mathbf{ テ }}x+\boxed{\mathbf{ ト }}$ である。
次に,$f(x)=ax^3+bx^2+cx+d$,$g(x)=\boxed{\mathbf{ テ }}x+\boxed{\mathbf{ ト }}$ とし,$f(x)-g(x)$ について考える。
$h(x)=f(x)-g(x)$ とおく。$a$,$b$,$c$,$d$ が正の実数であるとき,$y=h(x)$ のグラフの概形は $\boxed{\mathbf{ テ }}$ である。
$y=f(x)$ のグラフと $y=g(x)$ のグラフの共有点の $x$ 座標は $\displaystyle{\frac{\boxed{\mathbf{ ニヌ }}}{\boxed{\mathbf{ ネ }}}}$ と $\boxed{\mathbf{ ノ }}$ である。また,$x$ が $\displaystyle{\frac{\boxed{\mathbf{ ニヌ }}}{\boxed{\mathbf{ ネ }}}}$ と $\boxed{\mathbf{ ノ }}$ の間を動くとき,$|f(x)-g(x)|$ の値が最大となるのは,$\displaystyle{x=\frac{\boxed{\mathbf{ ハヒフ }}}{\boxed{\mathbf{ ヘホ }}}}$ のときである。
$\boxed{\mathbf{ ナ }}$ については,最も適当なものを,次の ⓪~⑤ のうちから一つ選べ。

$y=4x^3+2x^2+3x+5$ $\cdots\cdots$ (D)
$y=-2x^3+7x^2+3x+5$ $\cdots\cdots$ (E)
$y=5x^3-x^2+3x+5$ $\cdots\cdots$ (F)
(D) も (E) も (F) も $x=0$ を代入したら,$y=5$ となる
よって,$y$ 軸との交点の $y$ 座標は $\boxed{\mathbf{5}}$ である
(D) について微分すると $y’=12x^2+4x+3$
(E) について微分すると $y’=-6x^2+14x+3$
(F) について微分すると $y’=15x^2-2x+3$
どちらも $x=0$ における微分係数は $3$ となる
すなわち,$x=0$ における接線の傾きが $3$
接線は傾き $3$,$(0,5)$ を通るので,$y=\boxed{\mathbf{3}}x+\boxed{\mathbf{5}}$
曲線 $y=ax^3+bx^2+cx+d$ 上の点 $(0,\boxed{\mathbf{d}})$ における接線 $l$ について
$y’=3ax^2+2bx+c$ より,$x=0$ における微分係数(接線の傾き)は $c$
よって,接線 $l$ の方程式は $y=\boxed{\mathbf{c}}x+\boxed{\mathbf{d}}$ である
$f(x)=ax^3+bx^2+cx+d$,$g(x)=cx+d$ について,
\begin{eqnarray} h(x) &=& f(x)-g(x) = ax^3+bx^2 \end{eqnarray}導関数を求めると
$\displaystyle{h'(x)=3ax^2+2bx=3ax\left(x+\frac{2b}{3a}\right)}$
$h'(x)=0$ のとき
$\displaystyle{x=0,-\frac{2b}{3a}}$
$a>0$,$b>0$ より,$\displaystyle{-\frac{2b}{3a}<0}$
$a>0$ より $\displaystyle{h'(x)=3ax\left(x+\frac{2b}{3a}\right)}$ のグラフは下に凸で以下のようになる
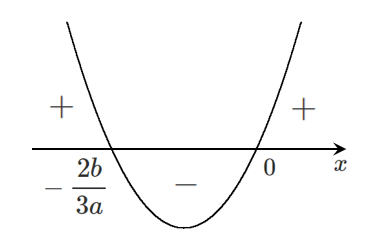
増減表をかくと
\begin{array}{c|ccccc} x & \cdots & -\frac{2b}{3a} & \cdots & 0 & \cdots \\ \hline h’(x) & + & 0 & – & 0 & + \\ \hline h(x) & \nearrow & & \searrow & 0 & \nearrow \end{array}増減表をもとに $h(x)$ のグラフをかくと
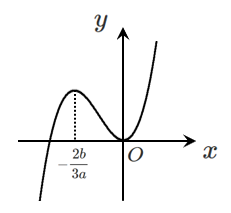
$x=0$ で極小値 $0$ をとるので,グラフの概形は $\boxed{\mathbf{②}}$
増減表の書き方はこれ↓

$y=f(x)$ のグラフと $y=g(x)$ のグラフの共有点の $x$ 座標は
$f(x)=g(x)$ より $f(x)-g(x)=0$ つまり $h(x)=0$ を満たすので
$ax^3+bx^2=0$
$x^2(ax+b)=0$
$ x=0 $,$\displaystyle{-\frac{b}{a}}$
$y=f(x)$ のグラフと $y=g(x)$ のグラフの共有点の $x$ 座標は $\displaystyle{\frac{\boxed{\mathbf{-b}}}{\boxed{\mathbf{a}}}}$ と $\boxed{\mathbf{0}}$
$x$ が $\displaystyle{\frac{\boxed{\mathbf{-b}}}{\boxed{\mathbf{a}}}}$ と $\boxed{\mathbf{0}}$ の間を動くとき,$h(x)>0$ であるから,
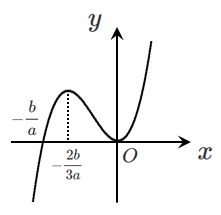
$|f(x)-g(x)|=|h(x)|=|ax^3+bx^2|$
の値が最大となるのは,$\displaystyle{x=\frac{\boxed{\mathbf{-2b}}}{\boxed{\mathbf{3a}}}}$ のとき
2021年度共通テストの大問
2021年度共通テスト数学ⅠA
- 第1問【1】数と式
- 第1問【2】図形と計量
- 第2問【1】2次関数
- 第2問【2】データの分析
- 第3問 場合の数と確率
- 第4問 整数の性質
- 第5問 図形の性質
2021年度共通テスト数学ⅡB
- 第1問【1】三角関数
- 第1問【2】指数関数・対数関数
- 第2問 微分法・積分法
- 第3問 確率分布と統計的な推測
- 第4問 数列
- 第5問 ベクトル

微分と積分の基本ができている受験生なら解ける!
基本を大切に!





コメント