2021共通テストⅠA第１問【２】180°-θ・正弦・余弦・面積

2021年度共通テスト数学ⅠAの第１問「図形と計量」の問題の解説！

解いたことがない人は解いてみよう！

問題
解答
1. (1)
2. (2)
3. (3)
4. (4)
問題で問われている力
2021年度共通テストの大問

問題

第１問

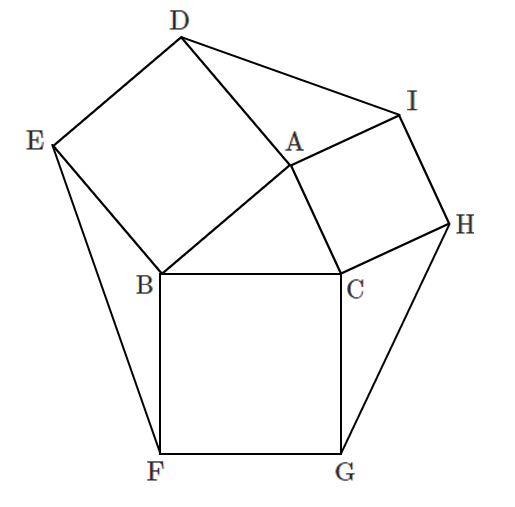[2]　右の図のように $\triangle \rm{ABC}$ の外側に辺 $\rm{AB}$，$\rm{BC}$，$\rm{CA}$ をそれぞれ $1$ 辺とする正方形 $\rm{ADEB}$，$\rm{BFGC}$，$\rm{CHIA}$ をかき，$2$ 点 $\rm{E}$ と $\rm{F}$，$\rm{G}$ と $\rm{H}$，$\rm{I}$ と $\rm{D}$，をそれぞれ線分で結んだ図形を考える。以下において

　$\rm{BC}=\it{a}$，$\rm{CA}=\it{b}$，$\rm{AB}=\it{c}$
　$\angle\rm{CAB}=\it{A}$，$\angle\rm{ABC}=\it{B}$，$\angle\rm{BCA}=\it{C}$

とする。

(1)　$b=6$，$c=5$，$\displaystyle{\cos A=\frac{3}{5}}$ のとき，$\displaystyle{\sin A=\frac{\boxed{\mathbf{　セ　}}}{\boxed{\mathbf{　ソ　}}}}$ であり，
$\triangle \rm{ABC}$ の面積は $\boxed{\mathbf{ タチ }}$，$\triangle \rm{AID}$ の面積は $\boxed{\mathbf{ ツテ }}$ である。

(2)　正方形 $\rm{BFGC}$，$\rm{CHIA}$，$\rm{ADEB}$ の面積をそれぞれ $S_1$，$S_2$，$S_3$ とする。
このとき，$S_1-S_2-S_3$ は

　　・$0^{\circ} < A < 90^{\circ}$ のとき，$\boxed{\mathbf{　ト　}}$。

　　・$A=90^{\circ}$ のとき，$\boxed{\mathbf{　ナ　}}$。

　　・$90^{\circ} < A < 180^{\circ}$ のとき，$\boxed{\mathbf{　ニ　}}$。

　$\boxed{\mathbf{　ト　}}$ ～ $\boxed{\mathbf{　ニ　}}$ の解答群（同じものを繰り返し選んでもよい。）

　 ⓪　$0$ である
　 ①　正の値である
　 ②　負の値である
　 ③　正の値も負の値もとる

(3)　$\triangle \rm{AID}$，$\triangle \rm{BEF}$，$\triangle \rm{CGH}$ の面積をそれぞれ $T_1$，$T_2$，$T_3$ とする。このとき，$\boxed{\mathbf{　ヌ　}}$ である。

　$\boxed{\mathbf{　ヌ　}}$ の解答群

　 ⓪　$a < b < c$ ならば，$T_1 > T_2 > T_3$
　 ①　$a < b < c$ ならば，$T_1 < T_2 < T_3$
　 ②　$A$ が鈍角ならば，$T_1 < T_2$ かつ $T_1 < T_3$
　 ③　$a$，$b$，$c$ の値に関係なく，$T_1=T_2=T_3$

(4)　$\triangle \rm{ABC}$，$\triangle \rm{AID}$，$\triangle \rm{BEF}$，$\triangle \rm{CGH}$ のうち，外接円の半径が最も小さいものを求める。

　　　$0^{\circ} < A < 90^{\circ}$ のとき， $\rm{ID} \boxed{\mathbf{　ネ　}} \rm{BC}$ であり

　　　（$\triangle \rm{AID}$ の外接円の半径）$\boxed{\mathbf{　ノ　}}$（$\triangle \rm{ABC}$ の外接円の半径）

　　であるから，外接円の半径が最も小さい三角形は

　　・$0^{\circ} < A < B < C < 90^{\circ}$ のとき，$\boxed{\mathbf{　ハ　}}$ である。

　　・$0^{\circ} < A < B < 90^{\circ} < C$ のとき，$\boxed{\mathbf{　ヒ　}}$ である。

　$\boxed{\mathbf{　ネ　}}$ ， $\boxed{\mathbf{　ノ　}}$ の解答群（同じものを繰り返し選んでもよい。）

　 ⓪　$<$　　　　①　$=$　　　　②　$>$

　$\boxed{\mathbf{　ハ　}}$ ， $\boxed{\mathbf{　ヒ　}}$ の解答群（同じものを繰り返し選んでもよい。）

　 ⓪　$\triangle \rm{ABC}$　　①　$\triangle \rm{AID}$　　②　$\triangle \rm{BEF}$　　③　$\triangle \rm{CGH}$

解答

(1)

\begin{eqnarray} \sin A &=& \sqrt{1-\cos^2 A} \\\\ &=& \sqrt{1-(\frac{3}{5})^2} \\\\ &=& \sqrt{\frac{16}{25}} \\\\ &=& \frac{4}{5} \end{eqnarray}

ポイント

　三角比の相互関係　$\sin^2A+\cos^2A=1$　を用いて $\cos A$ の値から $\sin A$ の値を求める

三角比の相互関係

三角比の相互関係３つ答えられますか？その３つはそれぞれどういう場面で使えるか理解していますか？三角比の相互関係が使いこなせれば， sin・cos・tanの内の１つから，他の値を求めることができます！鋭角か鈍角かに注意して使えれば，三角比の相互関係はばっちり！

　$\triangle \rm{ABC}$ の面積は

$\displaystyle{\frac{1}{2}bc\sin A=\frac{1}{2}\cdot6\cdot5\cdot\frac{4}{5}=12}$

ポイント

　三角形の面積の公式　$\displaystyle{S=\frac{1}{2}bc\sin A}$　を用いて面積を求める

三角形の面積

三角形の面積の公式といえば，「底辺×高さ÷２」しかし，三角形の面積を計算する問題で，底辺と高さがわかっているケースは少ないです！高校数学において，三角形の面積を求める際には，sinを用いた公式をよく使います！ sinを用いた三角形の面積の公式の使い方と証明をわかりやすく解説します！

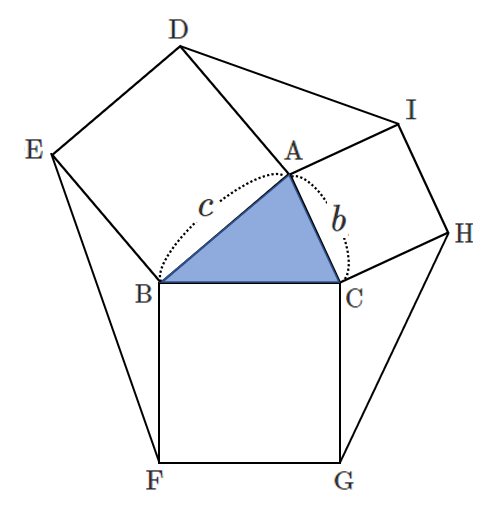
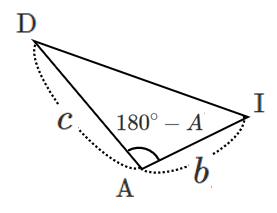
　$\rm{AI}=\it{b}$， $\rm{AD}=\it{c}$，$\angle \rm{IAD}=180^{\circ}-\it{A}$ より

　$\triangle \rm{AID}$ の面積は

\begin{eqnarray} \frac{1}{2}bc\sin (180^{\circ}-A) &=& \frac{1}{2}bc\sin A \\\\ &=& \frac{1}{2}\cdot6\cdot5\cdot\frac{4}{5} \\\\ &=& 12 \end{eqnarray}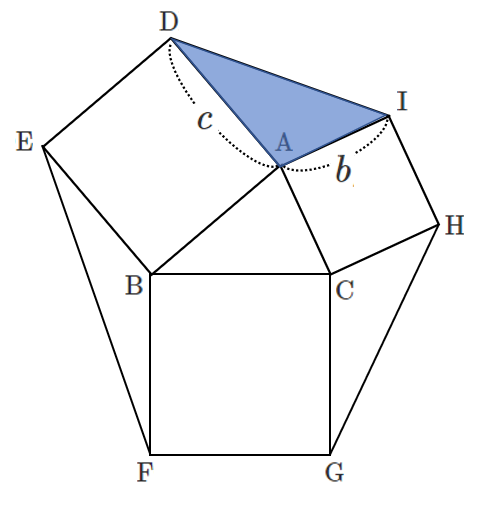

ポイント

　$180^{\circ}-A$ の三角比　$\sin (180^{\circ}-A)=\sin A$　を用いる

180°-θ の三角比

180°-θの三角比の公式覚えていますか？忘れがちな三角比の公式の一つです！式が複雑そうに見えるのが覚えにくい理由として挙げられます！式だけ見るのではなく，式の意味を理解することが大切です！この投稿を見れば，180°-θの公式をもう忘れません！

$180^{\circ}-A$ の三角比はよく出題されるよ！

$90^{\circ}-A$ の三角比もおさえておこう！

＜$180^{\circ}-\theta$ が出てくる図形＞

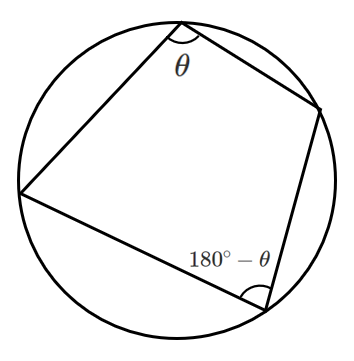
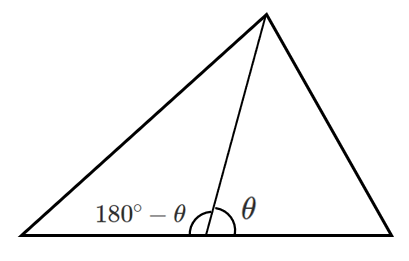
など

(2)

(2)　正方形 $\rm{BFGC}$，$\rm{CHIA}$，$\rm{ADEB}$ の面積をそれぞれ $S_1$，$S_2$，$S_3$ とする。
このとき，$S_1-S_2-S_3$ は

　　・$0^{\circ} < A < 90^{\circ}$ のとき，$\boxed{\mathbf{　ト　}}$。

　　・$A=90^{\circ}$ のとき，$\boxed{\mathbf{　ナ　}}$。

　　・$90^{\circ} < A < 180^{\circ}$ のとき，$\boxed{\mathbf{　ニ　}}$。

　$\boxed{\mathbf{　ト　}}$ ～ $\boxed{\mathbf{　ニ　}}$ の解答群（同じものを繰り返し選んでもよい。）

　 ⓪　$0$ である
　 ①　正の値である
　 ②　負の値である
　 ③　正の値も負の値もとる

　$S_1=a^2$，$S_2=b^2$，$S_3=c^2$ より

$S_1-S_2-S_3=a^2-b^2-c^2$

　$\triangle \rm{ABC}$ で余弦定理を用いると

$\displaystyle{\cos A=\frac{b^2+c^2-a^2}{2bc}}$

ポイント

　$\cos A$ の符号は，$b^2+c^2-a^2$　の符号と等しい

ポイント

$A$ が鋭角のとき，$\cos A > 0$

$A$ が直角のとき，$\cos A = 0$

$A$ が鈍角のとき，$\cos A < 0$

　・$0^{\circ} < A < 90^{\circ}$ のとき（$A$ が鋭角のとき）

$\cos A > 0$

　　$\cos A$ が正より

$b^2+c^2-a^2>0$

$a^2-b^2-c^2<0$

$S_1-S_2-S_3 < 0$

　　よって，$S_1-S_2-S_3$ は負である（②）

　・$A=90^{\circ}$ のとき（$A$ が直角のとき）

$\cos A = 0$

　　$\cos A$ が $0$ より

$b^2+c^2-a^2=0$

$a^2-b^2-c^2=0$

$S_1-S_2-S_3=0$

　　よって，$S_1-S_2-S_3$ は $0$ である（⓪）

　・$90^{\circ} < A < 180^{\circ}$ のとき（$A$ が鈍角のとき）

$\cos A < 0$

　　$\cos A$ が負より

$b^2+c^2-a^2<0$

$a^2-b^2-c^2>0$

$S_1-S_2-S_3 >0$

　　よって，$S_1-S_2-S_3$ は正である（①）

(3)

(3)　$\triangle \rm{AID}$，$\triangle \rm{BEF}$，$\triangle \rm{CGH}$ の面積をそれぞれ $T_1$，$T_2$，$T_3$ とする。このとき，$\boxed{\mathbf{　ヌ　}}$ である。

　$\boxed{\mathbf{　ヌ　}}$ の解答群

ポイント

　$180^{\circ}-A$ の三角比　$\sin (180^{\circ}-A)=\sin A$　を用いる

　(1) より，

$\triangle \rm{ABC}$ の面積と $\triangle \rm{AID}$ の面積 $T_1$ は等しい

　同様に，$\triangle \rm{BEF}$ の面積 $T_2$ は

$\displaystyle{T_2=\frac{1}{2}ca\cos (180^{\circ}-B)= \frac{1}{2}ca\cos B}$

　これは $\triangle \rm{ABC}$ の面積と等しい

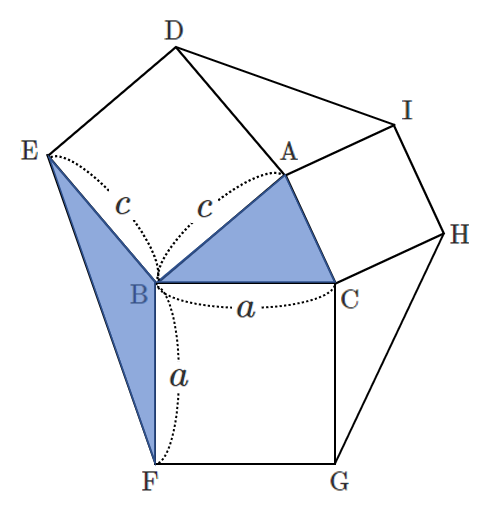
　また，$\triangle \rm{CGH}$ の面積 $T_3$ は

$\displaystyle{T_3=\frac{1}{2}ab\cos (180^{\circ}-C)= \frac{1}{2}ab\cos C}$

　これは $\triangle \rm{ABC}$ の面積と等しい

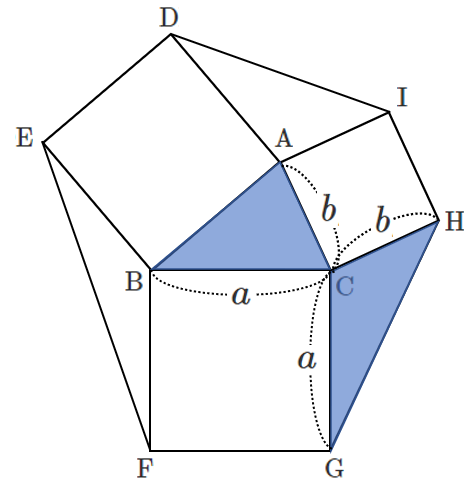
　したがって，$a$，$b$，$c$ の値に関係なく，$T_1=T_2=T_3$（③）

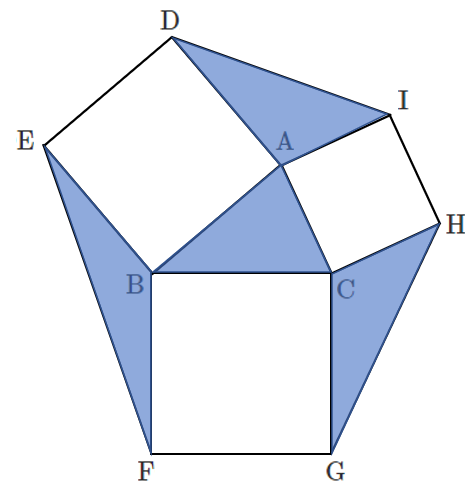
(4)

第１問

(4)　$\triangle \rm{ABC}$，$\triangle \rm{AID}$，$\triangle \rm{BEF}$，$\triangle \rm{CGH}$ のうち，外接円の半径が最も小さいものを求める。

　　　$0^{\circ} < A < 90^{\circ}$ のとき， $\rm{ID} \boxed{\mathbf{　ネ　}} \rm{BC}$ であり

　　　（$\triangle \rm{AID}$ の外接円の半径）$\boxed{\mathbf{　ノ　}}$（$\triangle \rm{ABC}$ の外接円の半径）

　　であるから，外接円の半径が最も小さい三角形は

　　・$0^{\circ} < A < B < C < 90^{\circ}$ のとき，$\boxed{\mathbf{　ハ　}}$ である。

　　・$0^{\circ} < A < B < 90^{\circ} < C$ のとき，$\boxed{\mathbf{　ヒ　}}$ である。

　$\boxed{\mathbf{　ネ　}}$ ， $\boxed{\mathbf{　ノ　}}$ の解答群（同じものを繰り返し選んでもよい。）

　 ⓪　$<$　　　　①　$=$　　　　②　$>$

　$\boxed{\mathbf{　ハ　}}$ ， $\boxed{\mathbf{　ヒ　}}$ の解答群（同じものを繰り返し選んでもよい。）

　 ⓪　$\triangle \rm{ABC}$　　①　$\triangle \rm{AID}$　　②　$\triangle \rm{BEF}$　　③　$\triangle \rm{CGH}$

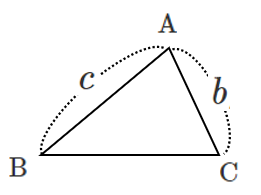
　$\triangle \rm{ABC}$ で余弦定理より

\begin{eqnarray} \rm{BC}^2 &=& b^2+c^2-2bc\cos A \\ \end{eqnarray}

　$\triangle \rm{AID}$ で余弦定理より

\begin{eqnarray} \rm{ID}^2 &=& b^2+c^2-2bc\cos (180^{\circ}-A) \\\\ &=& b^2+c^2-2bc(-\cos A) \\\\ &=& b^2+c^2+2bc\cos A \end{eqnarray}

ポイント

　$180^{\circ}-A$ の三角比　$\cos (180^{\circ}-A)=-\cos A$　を用いる

　$0^{\circ} < A < 90^{\circ}$ より，　$\cos A > 0$

　$2bc\cos A > 0$ なので

$\rm{BC}^2$ $= b^2+c^2-2bc\cos A$

$\rm{ID}^2 $ $ = b^2+c^2+2bc\cos A$

　の大小関係を比較すると，　$\rm{ID^2 > BC^2}$

　すなわち，　　　　　　　　$\rm{ID > BC}$（②）

　$\triangle \rm{ABC}$， $\triangle \rm{AID}$ の外接円の半径をそれぞれ $R$，$R_1$ とすると

　$\triangle \rm{ABC}$ で正弦定理より

\begin{eqnarray} 2R &=& \frac{\rm{BC}}{\sin A} \\\\ R &=& \frac{\rm{BC}}{2\sin A} \end{eqnarray}

　$\triangle \rm{AID}$ で正弦定理より

\begin{eqnarray} 2R_1 &=& \frac{\rm{ID}}{\sin (180^{\circ}-A)} \\\\ 2R_1 &=& \frac{\rm{ID}}{\sin A} \\\\ R_1 &=& \frac{\rm{ID}}{2\sin A} \end{eqnarray}

ポイント

　$180^{\circ}-A$ の三角比　$\sin (180^{\circ}-A)=\sin A$　を用いる

　$\displaystyle{R = \frac{\rm{BC}}{2\sin A}}$

$\displaystyle{R_1=\frac{\rm{ID}}{2\sin A}}$

　について大小関係を比較すると，

　$\rm{ID > BC}$ より，　　$R_1>R$（②）

　$\triangle \rm{BEF}$， $\triangle \rm{CGH}$ の外接円の半径をそれぞれ $R_2$，$R_3$ とすると

　・$0^{\circ} < A < B < C < 90^{\circ}$ のとき

　　前問より，

$0^{\circ} < A < 90^{\circ}$ のとき，　$R_1>R$

　　これと同様に，

$0^{\circ} < B < 90^{\circ}$ より，　$R_2>R$

$0^{\circ} < C < 90^{\circ}$ より，　$R_3>R$

　　以上より，$R$，$R_1$，$R_2$，$R_3$ の中から最も小さいのは　$R$（⓪）

　・$0^{\circ} < A < B < 90^{\circ} < C $ のとき

$0^{\circ} < A < B < 90^{\circ}$ より，　$R_1>R$，$R_2>R$

$90^{\circ} < C$ より，　$R_3<R$

　　以上より，$R$，$R_1$，$R_2$，$R_3$ の中から最も小さいのは　$R_3$（③）

問題で問われている力

2021年度共通テストの大問

2021年度共通テスト数学ⅠA

第１問【１】数と式
第１問【２】図形と計量
第２問【１】２次関数
第２問【２】データの分析
第３問　　　場合の数と確率
第４問　　　整数の性質
第５問　　　図形の性質

2021年度共通テスト数学ⅡB

第１問【１】三角関数
第１問【２】指数関数・対数関数
第２問　　　微分法・積分法
第３問　　　確率分布と統計的な推測
第４問　　　数列
第５問　　　ベクトル

対策すれば必ず解ける！

解けなかった問題はしっかり対策しよう！

2021年共通テストⅠA 第１問 [2] 図形と計量（本試）

問題

解答

(1)

(2)

(3)

(4)

問題で問われている力

2021年度共通テストの大問

コメント