
2021年度共通テスト数学ⅠAの第2問「2次関数」の問題の解説!
解いたことがない人は解いてみよう!
問題
第2問
[1] 陸上競技の短期距離 $100$ m 走では,$100$ m を走るのにかかる時間(以下,タイムと呼ぶ)は,$1$ 歩あたりの進む距離(以下,ストライドと呼ぶ)と $1$ 秒あたりの歩数(以下,ピッチと呼ぶ)に関係がある。ストライドとピッチはそれぞれ以下の式で与えられる。
\begin{eqnarray} ストライド(m/歩) = \frac{100(m)}{100 m を走るのにかかった歩数(歩)} \\\\ ピッチ(歩/秒) = \frac{100 m を走るのにかかった歩数(歩)}{タイム(秒)} \end{eqnarray}
ただし,$100$ m を走るのにかかった歩数は,最後の $1$ 歩がゴールラインをまたぐこともあるので,小数で表される。以下,単位は必要ない限り省略する。
例えば,タイムが $10.81$ で,そのときの歩数が $48.5$ であったとき,ストライドは $\displaystyle{\frac{100}{48.5}}$ より約 $2.06$,ピッチは $\displaystyle{\frac{48.5}{10.81}}$ より約 $4.49$ である。
(1) ストライドを $x$,ピッチを $z$ とおく。ピッチは $1$ 歩あたりの歩数,ストライドは $1$ 歩あたりの進む距離なので,$1$ 秒あたりの進む距離すなわち平均速度は,$x$ と $z$ を用いて $\boxed{\mathbf{ ア }}$ (m/秒) と表される。
これより,タイムと,ストライド,ピッチとの関係は
タイム $\displaystyle{=\frac{100}{\boxed{\mathbf{ ア }}}}$ $\cdots\cdots\cdots$ (Ⅰ)
と表されるので,$\boxed{\mathbf{ ア }}$ が最大になるときにタイムが最もよくなる。ただし,タイムがよくなるとは,タイムの値が小さくなることである。
$\boxed{\mathbf{ ア }}$ の解答群
⓪ $x+z$ ① $z-x$ ② $xz$
③ $\displaystyle{\frac{x+z}{2}}$ ④ $\displaystyle{\frac{z-x}{2}}$ ⑤ $\displaystyle{\frac{xz}{2}}$
(2) 男子短距離 $100$ m 走の選手である太郎さんは,(Ⅰ) に着目して,タイムが最もよくなるストライドとピッチを考えることにした。
次の表は,太郎さんが練習で $100$ m を $3$ 回走ったときのストライドとピッチのデータである。
| $1$ 回目 | $2$ 回目 | $3$ 回目 | |
|---|---|---|---|
| ストライド | $2.05$ | $2.10$ | $2.15$ |
| ピッチ | $4.70$ | $4.60$ | $4.50$ |
また,ストライドとピッチにはそれぞれ限界がある。太郎さんの場合,ストライドの最大値は $2.40$,ピッチの最大値は $4.80$ である。
太郎さんは,上の表から,ストライドが $0.05$ 大きくなるとピッチが $0.1$ 小さくなるという関係があると考えて,ピッチがストライドの $1$ 次関数として表されると仮定した。このとき,ピッチ $z$ はストライド $x$ を用いて
$\displaystyle{z=\boxed{\mathbf{ イウ }}x+\frac{\boxed{\mathbf{ エオ }}}{5}}$ $\cdots\cdots\cdots$ (Ⅱ)
と表される。
(Ⅱ)が太郎さんのストライドの最大値 $2.40$ とピッチの最大値 $4.80$ まで成り立つと仮定すると,$x$ の値の範囲は次のようになる。
$\boxed{\mathbf{ カ }}.\boxed{\mathbf{ キク }} ≦ x ≦ 2.40$
$y=\boxed{\mathbf{ ア }}$ とおく。(Ⅱ)を $y=\boxed{\mathbf{ ア }}$ に代入することにより,$y$ を $x$ の関数として表すことができる。太郎さんのタイムが最もよくなるストライドとピッチを求めるには,$\boxed{\mathbf{ カ }}.\boxed{\mathbf{ キク }} ≦ x ≦ 2.40$ の範囲で $y$ の値を最大にする $x$ の値を見つければよい。このとき,$y$ の値が最大になるのは $x=\boxed{\mathbf{ ケ }}.\boxed{\mathbf{ コサ }}$ のときである。
よって,太郎さんのタイムが最もよくなるのは,ストライドが $\boxed{\mathbf{ ケ }}.\boxed{\mathbf{ コサ }}$ のときであり,このとき,ピッチは $\boxed{\mathbf{ シ }}.\boxed{\mathbf{ スセ }}$ である。また,このときの太郎さんのタイムは,(Ⅰ)により $\boxed{\mathbf{ ソ }}$ である。
$\boxed{\mathbf{ ソ }}$ については,最も適当なものを,次の⓪~⑤のうちから一つ選べ。
⓪ $9.68$ ① $9.97$ ② $10.09$
③ $10.33$ ④ $10.42$ ⑤ $10.55$
解答と解説
(1)
[1] 陸上競技の短期距離 $100$ m 走では,$100$ m を走るのにかかる時間(以下,タイムと呼ぶ)は,$1$ 歩あたりの進む距離(以下,ストライドと呼ぶ)と $1$ 秒あたりの歩数(以下,ピッチと呼ぶ)に関係がある。ストライドとピッチはそれぞれ以下の式で与えられる。
\begin{eqnarray} ストライド(m/歩) = \frac{100(m)}{100 m を走るのにかかった歩数(歩)} \\\\ ピッチ(歩/秒) = \frac{100 m を走るのにかかった歩数(歩)}{タイム(秒)} \end{eqnarray}
ただし,$100$ m を走るのにかかった歩数は,最後の $1$ 歩がゴールラインをまたぐこともあるので,小数で表される。以下,単位は必要ない限り省略する。
例えば,タイムが $10.81$ で,そのときの歩数が $48.5$ であったとき,ストライドは $\displaystyle{\frac{100}{48.5}}$ より約 $2.06$,ピッチは $\displaystyle{\frac{48.5}{10.81}}$ より約 $4.49$ である。
(1) ストライドを $x$,ピッチを $z$ とおく。ピッチは $1$ 歩あたりの歩数,ストライドは $1$ 歩あたりの進む距離なので,$1$ 秒あたりの進む距離すなわち平均速度は,$x$ と $z$ を用いて $\boxed{\mathbf{ ア }}$ (m/秒) と表される。
これより,タイムと,ストライド,ピッチとの関係は
タイム $\displaystyle{=\frac{100}{\boxed{\mathbf{ ア }}}}$ $\cdots\cdots\cdots$ (Ⅰ)
と表されるので,$\boxed{\mathbf{ ア }}$ が最大になるときにタイムが最もよくなる。ただし,タイムがよくなるとは,タイムの値が小さくなることである。
$\boxed{\mathbf{ ア }}$ の解答群
⓪ $x+z$ ① $z-x$ ② $xz$
③ $\displaystyle{\frac{x+z}{2}}$ ④ $\displaystyle{\frac{z-x}{2}}$ ⑤ $\displaystyle{\frac{xz}{2}}$
ストライドを $x$ m/歩,ピッチを $z$ 歩/秒,$100$ mを走るのにかかった歩数を $a$ 歩,タイムを $t$ 秒とすると
$\displaystyle{x=\frac{100}{a}}$, $\displaystyle{z=\frac{a}{t}}$
辺々をかけあわせると
$\displaystyle{xz=\frac{100}{t}}$
$\displaystyle{\frac{100}{t}}$ は平均速度を表しているので,
平均速度は $x$ と $z$ を用いると $xz$(②) である
これより,
$\displaystyle{t=\frac{100}{xz}}$ $\cdots\cdots\cdots$ (Ⅰ)
<単位で考える方法>
小学校で習った「距離÷時間=速さ」を単位で表すと「m÷秒=m/秒」
というように,単位の式と必ず一致することがわかる
今回の問題にこれを応用する
ストライド(m/歩),ピッチ(歩/秒)を用いて平均速度(m/秒)を作るなら
$\displaystyle{\frac{m}{歩}\times\frac{歩}{秒}=\frac{m}{秒}}$
つまり,
ストライド×ピッチ=平均速度
と考えられる
(2)
(2) 男子短距離 $100$ m 走の選手である太郎さんは,(Ⅰ) に着目して,タイムが最もよくなるストライドとピッチを考えることにした。
次の表は,太郎さんが練習で $100$ m を $3$ 回走ったときのストライドとピッチのデータである。
| $1$ 回目 | $2$ 回目 | $3$ 回目 | |
|---|---|---|---|
| ストライド | $2.05$ | $2.10$ | $2.15$ |
| ピッチ | $4.70$ | $4.60$ | $4.50$ |
また,ストライドとピッチにはそれぞれ限界がある。太郎さんの場合,ストライドの最大値は $2.40$,ピッチの最大値は $4.80$ である。
太郎さんは,上の表から,ストライドが $0.05$ 大きくなるとピッチが $0.1$ 小さくなるという関係があると考えて,ピッチがストライドの $1$ 次関数として表されると仮定した。このとき,ピッチ $z$ はストライド $x$ を用いて
$\displaystyle{z=\boxed{\mathbf{ イウ }}x+\frac{\boxed{\mathbf{ エオ }}}{5}}$ $\cdots\cdots\cdots$ (Ⅱ)
と表される。
(Ⅱ)が太郎さんのストライドの最大値 $2.40$ とピッチの最大値 $4.80$ まで成り立つと仮定すると,$x$ の値の範囲は次のようになる。
$\boxed{\mathbf{ カ }}.\boxed{\mathbf{ キク }} ≦ x ≦ 2.40$
$y=\boxed{\mathbf{ ア }}$ とおく。(Ⅱ)を $y=\boxed{\mathbf{ ア }}$ に代入することにより,$y$ を $x$ の関数として表すことができる。太郎さんのタイムが最もよくなるストライドとピッチを求めるには,$\boxed{\mathbf{ カ }}.\boxed{\mathbf{ キク }} ≦ x ≦ 2.40$ の範囲で $y$ の値を最大にする $x$ の値を見つければよい。このとき,$y$ の値が最大になるのは $x=\boxed{\mathbf{ ケ }}.\boxed{\mathbf{ コサ }}$ のときである。
よって,太郎さんのタイムが最もよくなるのは,ストライドが $\boxed{\mathbf{ ケ }}.\boxed{\mathbf{ コサ }}$ のときであり,このとき,ピッチは $\boxed{\mathbf{ シ }}.\boxed{\mathbf{ スセ }}$ である。また,このときの太郎さんのタイムは,(Ⅰ)により $\boxed{\mathbf{ ソ }}$ である。
$\boxed{\mathbf{ ソ }}$ については,最も適当なものを,次の⓪~⑤のうちから一つ選べ。
⓪ $9.68$ ① $9.97$ ② $10.09$
③ $10.33$ ④ $10.42$ ⑤ $10.55$
$z$(ピッチ) が $x$(ストライド)の $1$ 次関数だとすると
| $x$ | $2.05$ | $2.10$ | $2.15$ |
| $z$ | $4.70$ | $4.60$ | $4.50$ |
$(2.05,4.70)$, $(2.10,4.60)$ を通る直線と考えることができる
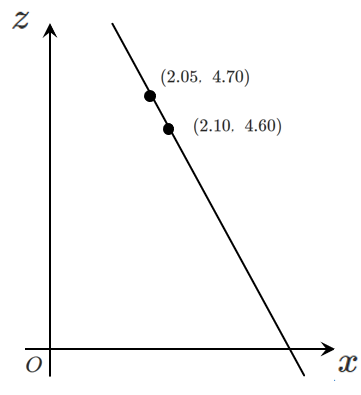
傾きは $\displaystyle{\frac{4.60-4.70}{2.10-2.05}=-2}$
点 $(2.05,4.70)$ を通るので
$z-4.70=-2(x-2.05)$
$z=-2x+8.8$
$\displaystyle{z=-2x+\frac{44}{5}}$ $\cdots\cdots\cdots$ (Ⅱ)
このグラフは単調減少するので,
$z$(ピッチ)の最大値 $4.80$ のとき,$x$(ストライド)は最小になる
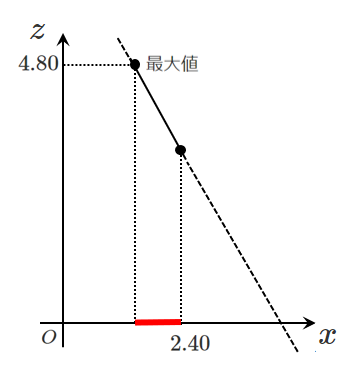
$z=4.8$ のとき, $x=2.00$
したがって, $2.00 ≦ x ≦ 2.40$
$y=xz$ とすると, $\displaystyle{z=-2x+\frac{44}{5}}$ を代入して
\begin{eqnarray} y &=& x\left(-2x+\frac{44}{5}\right) \\\\ &=& -2x^2+\frac{44}{5}x \\\\ &=& -2(x^2-\frac{22}{5}x) \\\\ &=& -2\left(x-\frac{11}{5}\right)^2+\frac{242}{25} \end{eqnarray}軸 $\displaystyle{x=\frac{11}{5}=2.20}$ と定義域 $2.00 ≦ x ≦ 2.40$ の位置関係を調べると
$\displaystyle{2.00 < 2.20 < 2.40}$ より,軸は定義域の内側にあるので
$y$ の値が最大になるのは $x=2.20$ のとき
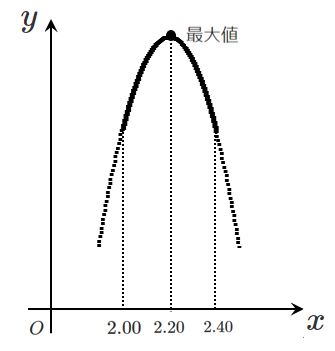
このときの $z$(ピッチ)は $z=-2x+8.8$ に $x=2.20$ を代入して
$z=4.40$
このときのタイムは(Ⅰ) より
$\displaystyle{t=\frac{100}{2.2\cdot4.4}=\frac{100}{9.68}≒10.330\cdots}$ (③)
問われている力
- $1$ 次関数
- $2$ 次関数の最大値
- 文章を読み取る力
2021年度共通テストの大問
2021年度共通テスト数学ⅠA
- 第1問【1】数と式
- 第1問【2】図形と計量
- 第2問【1】2次関数
- 第2問【2】データの分析
- 第3問 場合の数と確率
- 第4問 整数の性質
- 第5問 図形の性質
2021年度共通テスト数学ⅡB
- 第1問【1】三角関数
- 第1問【2】指数関数・対数関数
- 第2問 微分法・積分法
- 第3問 確率分布と統計的な推測
- 第4問 数列
- 第5問 ベクトル

長い文章を読み取って問題を解く力をつけよう!




コメント