『2次関数の決定』とは
2次関数の軸や頂点や通る点が与えられているとき,その2次関数を求める
という問題のことです!
『2次関数の決定』の問題を解くには,2次関数の『基本形』と『一般形』を使い分ける必要がありますが,
加えて『因数分解形』を使うことで,より効率的に問題を解くことができる場合があります!
この投稿を見れば,因数分解形を用いた『2次関数の決定』の問題は完璧!
問題
問題
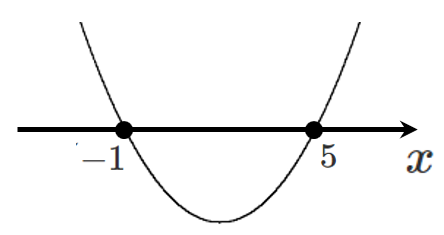
$x$ 軸と $(-1,0)$,$(5,0)$ で交わり,$(0,5)$ を通る2次関数を求めよ。
$x$ 軸と $(-1,0)$,$(5,0)$ で交わるので
$y=a(x+1)(x-5)$ ($a≠0$) とおくと
$(0,5)$ を通るので $5=a(0+1)(0-5)$
これを解いて $a=-1$
求める2次関数は $y=-(x+1)(x-5)$
2次関数の表し方
2次関数の表し方
① $y=ax^2+bx+c$ 【一般形】
② $y=a(x-p)^2+q$ 【基本形】 軸・頂点がわかる式
③ $y=a(x-\alpha)(x-\beta)$ 【因数分解形】 $x$ 軸との共有点がわかる式
② $y=a(x-p)^2+q$ 【基本形】 軸・頂点がわかる式
③ $y=a(x-\alpha)(x-\beta)$ 【因数分解形】 $x$ 軸との共有点がわかる式
基本形 $y=a(x-p)^2+q$
基本形のポイント
軸や頂点が条件として与えられている場合は,基本形 $y=a(x-p)^2+q$ を用いる
一般形 $y=ax^2+bx+c$
一般形のポイント
通る3点が与えられている場合は,一般形 $y=ax^2+bx+c$ を用いる
↓↓【基本形】と【一般形】の解説はこれ↓↓

2次関数の決定|基本形と一般形
『2次関数の決定』とは
2次関数の軸や頂点や通る点が与えられているとき,
その2次関数を求めるという問題のことです!
『2次関数の決定』の問題を解くには
2次関数の『基本形』と『一般形』を使い分ける必要があります!
この投稿を見れば,『2次関数の決定』の問題は完璧!
因数分解形 $y=a(x-\alpha)(x-\beta)$
因数分解形のポイント
$x$ 軸との共有点が与えられている場合は,因数分解形 $y=a(x-\alpha)(x-\beta)$ を用いる
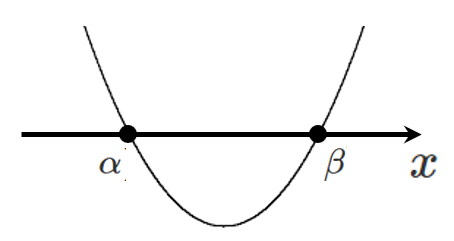


今回の問題は,3点が与えられている場合なので
【一般形 $y=ax^2+bx+c$】を利用して解くことができるけど,
$x$ 軸との共有点が与えられているので
【因数分解形】を利用する方が簡単に解けるよ!
復習
問題
$x$ 軸と $(-1,0)$,$(5,0)$ で交わり,$(0,5)$ を通る2次関数を求めよ。
解答
$x$ 軸と $(-1,0)$,$(5,0)$ で交わるので
$y=a(x+1)(x-5)$ ($a≠0$) とおくと
$(0,5)$ を通るので $5=a(0+1)(0-5)$
これを解いて $a=-1$
求める2次関数は $y=-(x+1)(x-5)$

あなたのオススメ
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント