高校数学Ⅰの2次関数の応用問題である『2次関数のグラフと係数の符号』に関する問題の解説です!
2次関数のグラフに関する基本が定着していれば、簡単に解くことができます!
問題
次の図は2次関数 $y=ax^2+bx+c$ のグラフである。このとき,次の値は正,0,負のいずれになるか。
(1) $a$
(2) $b$
(3) $c$
(4) $b^2-4ac$
(5) $a+b+c$
(6) $a-b+c$
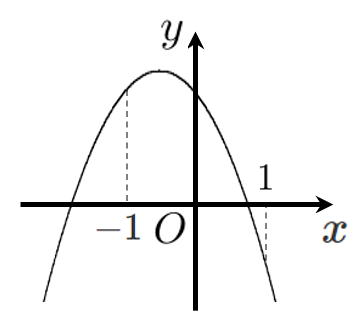
(1) $a$ の正負 ➡ 上に凸か下に凸か
グラフは上に凸なので $a$ は負
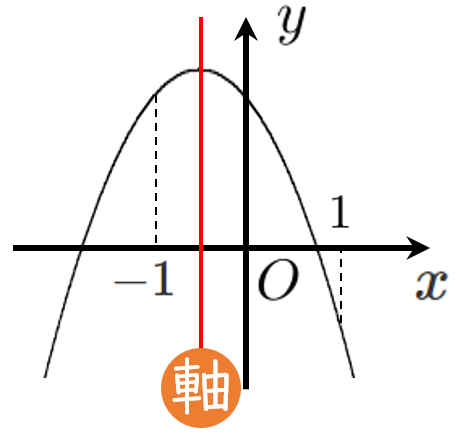
(2) $b$ の正負 ➡ 軸 $\displaystyle{x=-\frac{b}{2a}}$ の位置
軸 $\displaystyle{-\frac{b}{2a}}$ は負で $a$ は負なので $b$ は負
(3) $c$ の正負 ➡ $y$ 軸との交点の座標
グラフは $y$ 軸と正の部分で交わるので $c$ は正
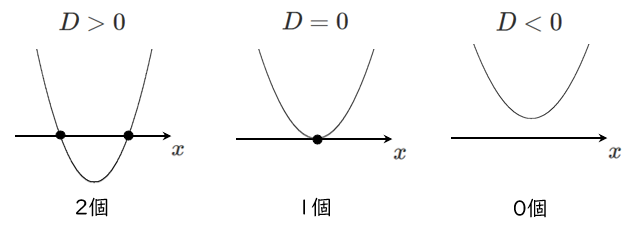
(4) $b^2-4ac$ の正負 ➡ グラフと $x$ 軸の共有点の個数
$b^2-4ac$ は判別式 $D$ で、異なる2点で交わっているので $b^2-4ac$ は正
(5) $a+b+c$ の正負 ➡ $x=1$ のときの $y$ 座標
グラフは $x=1$ のとき $x$ 軸より下なので $a+b+c$ は負
(6) $a-b+c$ の正負 ➡ $x=-1$ のときの $y$ 座標
グラフは $x=-1$ のとき $x$ 軸より上なので $a+b+c$ は正
$a$ の符号の決定
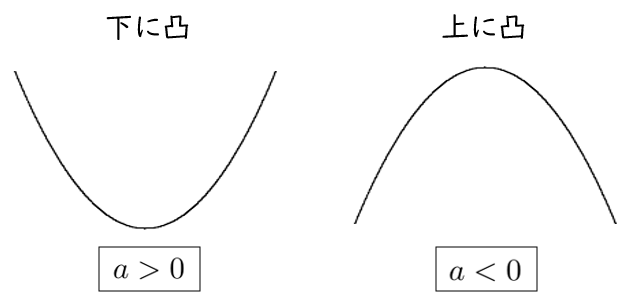
今回の問題は、
下に凸なので、$a$ は 負 である

$b$ の符号の決定
<補足>
$y=ax^2+bx+c$ を平方完成すると $\displaystyle{y=a\left(x+\frac{b}{2a}\right)^2-\frac{b^2-4ac}{4a}}$
となるので、軸は $\displaystyle{x=-\frac{b}{2a}}$
今回の問題は、
軸の位置が $y$ 軸より左側であることから、軸は 負
すなわち $\displaystyle{-\frac{b}{2a}}$ は 負
$a$ が負であることから、次のように考えられる
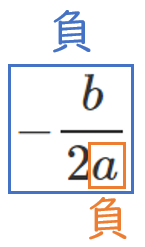
$a$ が負なので、$\displaystyle{-\frac{b}{2a}}$ が負になるように $b$ の符号を考えると
$b$ は 負 である
$c$ の符号の決定
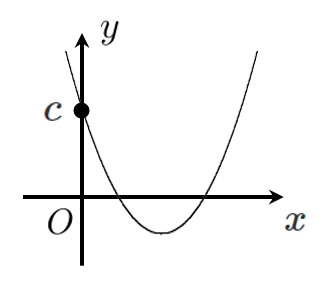
今回の問題は、
グラフと $y$ 軸の交点の座標は 正 なので、$c$ は 正 である
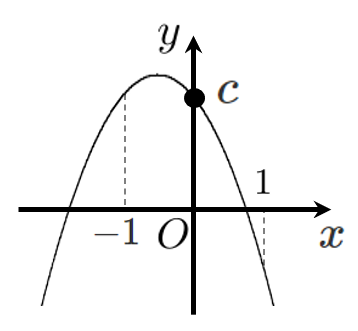
$b^2-4ac$ の符号の決定
今回の問題は、
グラフと $x$ 軸の共有点の個数は2個なので、$b^2-4ac$ は 正 である
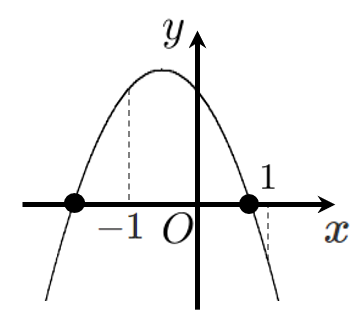
$a+b+c$ の符号の決定
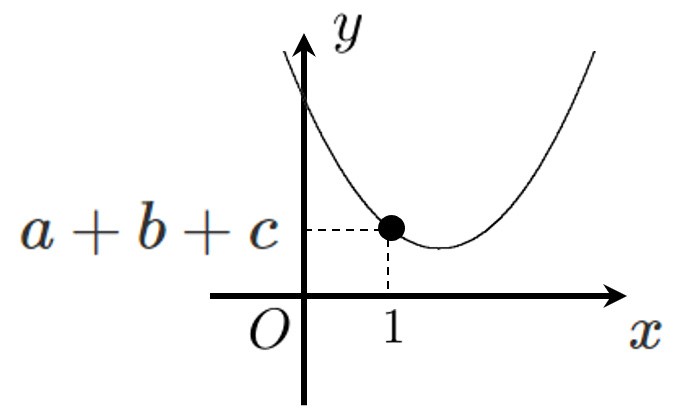
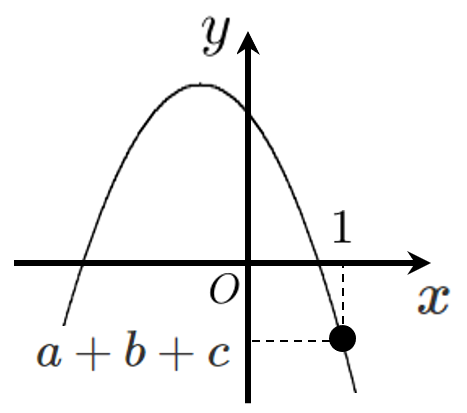
$y=ax^2+bx+c$ に $x=1$ を代入すると、$y=a+b+c$ である
今回の問題は、
$x=1$ のときの $y$ 座標が 負 なので、$a+b+c$ は 負 である
$a-b+c$ の符号の決定
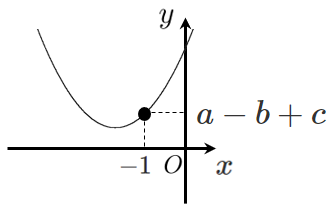
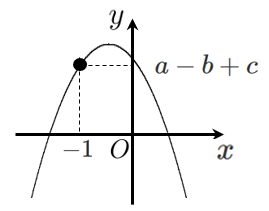
$y=ax^2+bx+c$ に $x=-1$ を代入すると、$y=a-b+c$ である
今回の問題は、
$x=-1$ のときの $y$ 座標が 正 なので、$a-b+c$ は 正 である
まとめ
| $a$ の符号 | グラフの形(下に凸か上に凸か) |
| $b$ の符号 | 軸の位置(軸 $\displaystyle{-\frac{b}{2a}}$ の符号と $a$ の符号) |
| $c$ の符号 | $y$ 軸との交点の座標 |
| $b^2-4ac$ の符号 | グラフと $x$ 軸の共有点の個数($b^2-4ac$ は判別式 $D$) |
| $a+b+c$ の符号 | $x=1$ のときの $y$ 座標 |
| $a-b+c$ の符号 | $x=-1$ のときの $y$ 座標 |
🔵2次関数のグラフの平行移動・対称移動
🔴軸に定数を含む2次関数の最大・最小の場合分け
🔴定義域の片端に定数を含む2次関数の最大・最小の場合分け
🔴定義域の両端に定数を含む2次関数の最大・最小の場合分け
🔵因数分解形の利用した2次関数の決定
🔴場合分けが必要な文字係数の方程式
🔵2次関数がx軸から切り取る線分の長さ
🔵絶対不等式
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント