4次式といった高次の式に、無理数(ルートを含む数)を代入する計算は非常に大変です!
しかし、高校数学Ⅱで学んだ整式の除法を利用することで、無理数の代入の計算が楽にできます!
この投稿では、高次の式に無理数を簡単に代入して計算する方法をわかりやすく解説します!
問題
$x=\sqrt{2}-1$ のとき、$P(x)=x^4+4x^3+5x^2+4x+1$ の値を求めよ。
解答
4次式 $P(x)$ にそのまま $x=\sqrt{2}-1$ を代入すると計算が大変
➡次数の低い式に代入できるように、$P(x)$ を式変形する(次数を下げる)
<解答の手順>
1. $x=\sqrt{2}-1$ を解にもつ2次方程式をつくる

2. 4次式 $P(x)$ を手順1の2次式で割り、$P(x)=$(2次式)×(商)+(余り) に変形する
3. $P(x)$ に $x=\sqrt{2}-1$ を代入すると、余りに代入するだけでよい

<解答>
$x=\sqrt{2}-1$ より $x+1=\sqrt{2}$
両辺を2乗すると $x^2+2x+1=2$
すなわち $x^2+2x-1=0$ … ①
$P(x)$ を $x^2+2x-1$ で割ると
右の計算より
商は $x^2+2x+2$
余りは $2x+3$
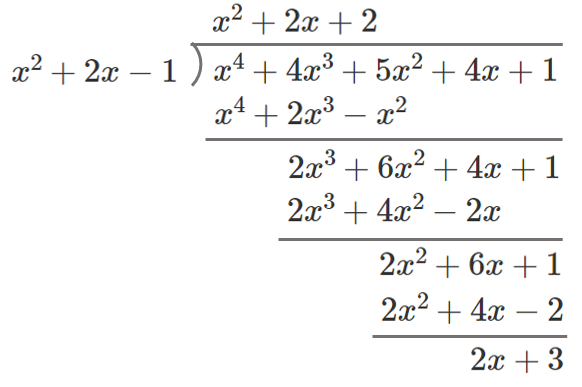
よって、 $P(x)=(x^2+2x-1)(x^2+2x+2)+2x+3$ ← $A=BQ+R$
2次方程式①の解の1つは $x=\sqrt{2}-1$ なので、
$x=\sqrt{2}-1$ のとき、$x^2+2x-1=0$ であるから
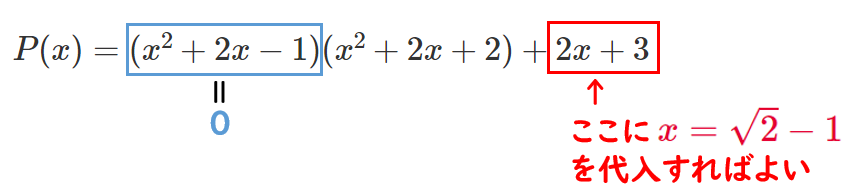
$P(\sqrt{2}-1)=2(\sqrt{2}-1)+3=2\sqrt{2}+1$ ←余り $2x+3$ に代入
あなたのオススメ




コメント