2次関数とx軸の位置関係は3種類!
おまけに,2次方程式の解の種類を判別する判別式Dとも深い関係が!
このことを理解しておけば,あらゆる場面で応用ができます!
この投稿を見れば,2次関数とx軸の位置関係と判別式Dの関係をわかりやすく学べます!
2次関数とx軸の位置関係

2次関数とx軸の位置関係は3種類あるよ!
[1] x軸と異なる2点で交わる
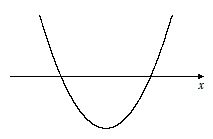
[2] x軸と接する(1点で交わる)
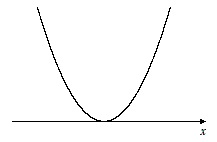
[3] x軸と交わらない
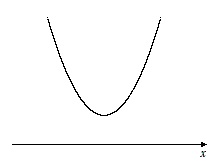

覚えなくても図をかけば3種類あることが分かるね!
2次関数とx軸の位置関係と2次方程式の実数解

『2次関数と $x$ 軸の位置関係』と『2次方程式の実数解』には切っても切れない関係があるよ!
●2次関数 $y=x^2-3x-4$ と $x$ 軸の位置関係
$x$ 軸との共有点を求めてみると
$y=0$ を代入して
$x^2-3x-4=0$
$(x+1)(x-4)=0$
$x=-1,4$
2次関数 $y=x^2-3x-4$ と $x$ 軸は,異なる2点で交わる
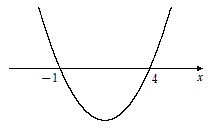
2次方程式 $x^2-3x-4=0$ の実数解が2個
2次関数 $y=x^2-3x-4$ と $x$ 軸が異なる2点で交わる
●2次関数 $y=x^2-4x+4$ と $x$ 軸の位置関係
$x$ 軸との共有点を求めてみると
$y=0$ を代入して
$x^2-4x+4=0$
$(x-2)^2=0$
$x=2$
2次関数 $y=x^2-4x+4$ と $x$ 軸は,接する(1点で交わる)
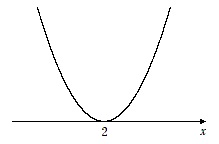
2次方程式 $x^2-4x+4=0$ の実数解が1個
2次関数 $y=x^2-4x+4$ と $x$ 軸が接する(1点で交わる)
●2次関数 $y=x^2-x+3$ と $x$ 軸の位置関係
$x$ 軸との共有点を求めてみると
$y=0$ を代入して
$x^2-x+3=0$
$\displaystyle{x=\frac{1±\sqrt{-11}}{2}}$
$\sqrt{ }$ の中に負の数が入るので実数解はない
2次関数 $y=x^2-x+3$ と $x$ 軸は,交わらない
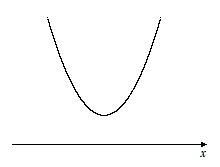
2次方程式 $x^2-x+3=0$ の実数解が0個
2次関数 $y=x^2-x+3$ と $x$ 軸は交わらない
2次関数と $x$ 軸の共有点を求めるときには2次関数に $y=0$ を代入する
$y=0$ を代入することで2次方程式になります
その2次方程式の解が共有点の座標になるので,
2次方程式の実数解の個数が2次関数と $x$ 軸の共有点の個数になります
2次方程式 $ax^2+bx+c=0$ の実数解の個数と等しい
2次関数とx軸の位置関係と判別式

2次方程式の実数解の個数はどうやったら調べられるのかな?

2次関数 $y=ax^2+bx+c$ と $x$ 軸の共有点の個数も判別式で調べられる
● $D>0$ のとき
2次方程式 $ax^2+bx+c=0$ の実数解の個数は2個
2次関数 $y=ax^2+bx+c$ と $x$ 軸の共有点の個数は2個

● $D=0$ のとき
2次方程式 $ax^2+bx+c=0$ の実数解の個数は1個(重解)
2次関数 $y=ax^2+bx+c$ と $x$ 軸の共有点の個数は1個(接する)

● $D<0$ のとき
2次方程式 $ax^2+bx+c=0$ の実数解の個数は0個
2次関数 $y=ax^2+bx+c$ と $x$ 軸の共有点の個数は0個

2次方程式 $ax^2+bx+c=0$ の判別式を $D$ とすると
$D>0$ のとき 異なる2点で交わる
$D=0$ のとき 接する(1点で交わる)
$D<0$ のとき 交わらない
2次関数 $y=x^2-3x+k$ について次のような条件を満たす $k$ の値の範囲を求めよ。
(1) $x$ 軸と異なる2点で交わる
(2) $x$ 軸と交わらない
(1) $x$ 軸と異なる2点で交わる
$y=0$ を代入する
2次方程式 $x^2-3x+k=0$ の判別式を $D$ とすると
\begin{eqnarray} D &=& (-3)^2-4・1・k \\\\ &=& 9-4k \end{eqnarray}$D>0$ より
$9-4k>0$
$\displaystyle{k<\frac{9}{4}}$
(2) $x$ 軸と交わらない
$D<0$ より
$9-4k<0$
$\displaystyle{k>\frac{9}{4}}$
2次関数 $y=x^2-6x+k$ が $x$ 軸と接するような $k$ の値を求めよ。
また,そのときの接点の座標を求めよ。
$y=0$ を代入する
2次方程式 $x^2-6x+k=0$ の判別式を $D$ とすると
\begin{eqnarray} D &=& (-6)^2-4・1・k \\\\ &=& 36-4k \end{eqnarray}$D=0$ より
$36-4k=0$
$k=9$
このとき
$x^2-6x+9=0$
$(x-3)^2=0$
$x=3$
接点の座標は $(3,0)$
まとめ
2次関数 $y=ax^2+bx+c$ に $y=0$ を代入した
2次方程式 $ax^2+bx+c=0$ の判別式を $D=b^2-4ac$ とすると
2次関数 $y=ax^2+bx+c$ と $x$ 軸の位置関係は
$D>0$ のとき 異なる2点で交わる
$D=0$ のとき 接する(1点で交わる)
$D<0$ のとき 交わらない
共有点をもつ場合は,$D>0$ または $D=0$ なので $D≧0$ である
以上のように,判別式 $D$ によって2次関数と $x$ 軸の位置関係が調べられる
$b$ が偶数のとき,$\displaystyle{\frac{D}{4}=(bの半分)^2-ac}$ を用いると簡単に計算ができる
問題
問題1
2次関数 $y=2x^2-5x+k$ が $x$ 軸と共有点をもつような $k$ の値の範囲を求めよ。
問題2
2次関数 $y=4x^2-12x+k$ が $x$ 軸と接するような $k$ の値を求めよ。
また,そのときの接点の座標を求めよ。
解答
問題1
$y=0$ を代入する
2次方程式 $2x^2-5x+k=0$ の判別式を $D$ とすると
\begin{eqnarray} D &=& (-5)^2-4・2・k \\\\ &=& 25-8k \end{eqnarray}$D≧0$ より
$25-8k≧0$
$\displaystyle{k≦\frac{25}{8}}$
問題2
$y=0$ を代入する
2次方程式 $4x^2-12x+k=0$ の判別式を $D$ とすると
\begin{eqnarray} D &=& (-12)^2-4・4・k \\\\ &=& 144-16k \end{eqnarray}$D=0$ より
$144-16k=0$
$k=9$
このとき
$4x^2-12x+9=0$
$(2x-3)^2=0$
$\displaystyle{x=\frac{3}{2}}$
接点の座標は $\displaystyle{\left(\frac{3}{2},0\right)}$
$\displaystyle{\frac{D}{4}}$ を用いた別解
\begin{eqnarray} \frac{D}{4} &=& (-6)^2-4・k \\\\ &=& 36-4k \end{eqnarray}$D=0$ より
$36-4k=0$
$k=9$

2次関数と $x$ 軸の位置関係にも判別式 $D$ が使えることは非常に大切!
しっかりおさえておこう!
🔰定義域における最大・最小
🔰2次方程式の実数解の個数と判別式
🔵2次関数のグラフと係数の符号
🔵2次関数がx軸から切り取る線分の長さ
🔰2次不等式|因数分解
🔰2次不等式|解の公式
🔰2次不等式|接する
🔰2次不等式|交わらない
🔰2次不等式|x²の係数が負
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!





コメント