高校数学Ⅱで学ぶ『2直線の交点を通る直線』について解説!
難しいと感じている高校生が多いテーマです!
この投稿を見れば、『2直線の交点を通る直線』はバッチリ!
2直線の交点を通る直線
2直線 $ax+by+c$$=0$,$a’x+b’y+c’$$=0$ の交点を通る直線は、実数 $k$ を用いて
$($$ax+by+c$$)+k($$a’x+b’y+c’$$)=0$
ただし、$a’x+b’y+c’=0$ を除く
例えば、
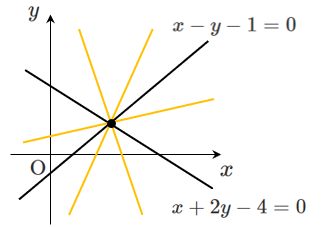
2直線 $x+2y-4$$=0$ と $x-y-1$$=0$ の交点を通る直線は
$($$x+2y-4$$)+k($$x-y-1$$)=0$ と表せる
ただし、$x-y-1=0$ を除く
$(x+2y-4)+k(x-y-1)=0$ を変形すると
$(k+1)x+(2k-1)y-4k-1=0$
係数 $k+1$,$2k-1$ は同時に $0$ になることはないので,
$(x+2y-4)+k(x-y-1)=0$ は $x$,$y$ の1次方程式であり,直線を表す
2直線 $x+2y-4=0$ と $x-y-1=0$ の交点は
\begin{eqnarray} \left\{ \begin{array}{l} x+2y-4=0 \\ x-y-1=0 \end{array} \right. \end{eqnarray}の解なので,交点は $(2,1)$
$(x+2y-4)+k(x-y-1)=0$ に $(2,1)$ を代入すると
$(2+2\cdot1-4)+k(2-1-1)=0$
等式が成り立つので,
直線 $(x+2y-4)+k(x-y-1)=0$ は,2直線 $x+2y-4=0$ と $x-y-1=0$ の交点 $(2,1)$ を通る
$(2,1)$ を通る直線は無数に存在します。
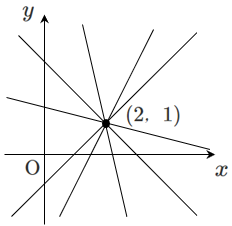
その無数に存在する直線(直線群という)を $(x+2y-4)+k(x-y-1)=0$ という1つの方程式でまとめています。(ただし,$x-y-1=0$ を除く)
$k$ の値が定まれば、1本に定まります。
例えば,
$k=1$ のときは $2x+y-5=0$
$k=-2$ のときは $x-4y+2=0$
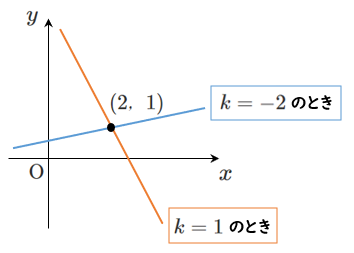
ただし,$k$ にどのような値を代入しても $x-y-1=0$ だけは表すことができない
2直線の交点を通る直線に関する問題
2直線 $4x+3y+2=0$,$5x-2y-3=0$ の交点を通る直線は,実数 $k$ を用いて
$(4x+3y+2)+k(5x-2y-3)=0$ … ① とおける
この直線が $(-1,-2)$ を通るので
$\{4\cdot(-1)+3\cdot(-2)+2\}+k\{5\cdot(-1)-2\cdot(-2)-3\}=0$
これを解いて $k=-2$
①に代入して $6x-7y-8=0$
定点を通る直線
$(k-1)x+(2k+1)y-5k+2=0$ を $k$ について整理すると
$(-x+y+2)+k(x+2y-5)=0$
この式は $-x+y+2=0$ かつ $x+2y-5=0$
のとき,$k$ の値にかかわらず成り立つ
これを解いて $x=3$,$y=1$
よって,求める定点の座標は $(3,1)$




コメント