高校数学Ⅱで習う『平面座標における線対称な点』に関する問題を解説!
成り立つための条件を整理して、式を作ることがポイント!
この投稿を見れば、『平面座標における線対称な点』はバッチリ!
直線に関して対称な点
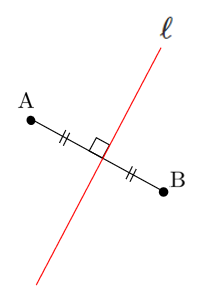
2点 $\textrm{A}$,$\textrm{B}$ が直線 $\ell$ に関して対称であるのは,次の [1],[2] が成り立つときである
[1] 直線 $\textrm{AB}$ は $\ell$ に垂直である
[2] 線分 $\textrm{AB}$ の中点は $\ell$ 上にある
問題
[1] 直線 $\textrm{AB}$ は $\ell$ に垂直である
(直線 $\textrm{AB}$ の傾き)$\cdot$(直線 $\ell$ の傾き)$=-1$ ← 垂直条件
[2] 線分 $\textrm{AB}$ の中点は $\ell$ 上にある
点 $\textrm{A}(x_1,y_1)$,$\textrm{B}(x_2,y_2)$ について,線分 $\textrm{AB}$ の中点は $\displaystyle{\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)}$
これを 直線 $\ell$ に代入する
点 $\textrm{B}$ の座標を $(p,q)$ とする
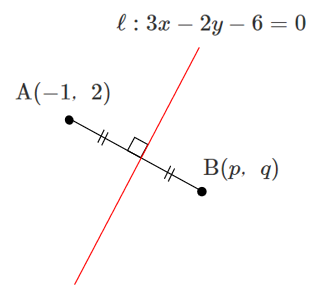
[1] 直線 $\ell$ を式変形すると $\displaystyle{y=\frac{3}{2}x-3}$ より,傾きは $\displaystyle{\frac{3}{2}}$
直線 $\textrm{AB}$ の傾きは $\displaystyle{\frac{q-2}{p-(-1)}}$
直線 $\ell$ と直線 $\textrm{AB}$ は垂直であるから
$\displaystyle{\frac{q-2}{p-(-1)}\cdot\frac{3}{2}=-1}$
すなわち $2p+3q=4$ … ①
[2] 線分 $\textrm{AB}$ の中点 $\displaystyle{\left(\frac{p+(-1)}{2},\frac{q+2}{2}\right)}$ が直線 $l$ 上にあるから
$\displaystyle{3\cdot\frac{p-1}{2}-2\cdot\frac{q+2}{2}-6=0}$
すなわち $3p-2q=19$ … ②
①,②を解くと $p=5$,$q=-2$
したがって,点 $\textrm{B}$ の座標は $(5,-2)$




コメント