高校数学Ⅱ『図形と方程式』で学ぶ『円が直線から切り取る弦の長さ』について解説!
弦の長さは、円の中心と弦の距離を求めて三平方の定理で求めることができます!
解と係数の関係を使った解法もあります!
この投稿を見れば、『円が直線から切り取る弦の長さ』はバッチリ!
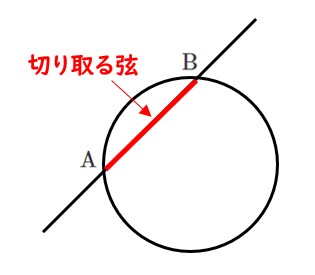
円が直線から切り取る弦とは
円と直線の交点を $\textrm{A}$,$\textrm{B}$ とするとき,
線分 $\textrm{AB}$ を「円が直線から切り取る弦」という。
円が直線から切り取る弦の長さの求め方
円と直線の交点を $\textrm{A}$,$\textrm{B}$ とする
円の中心 $\textrm{O}$ から直線に垂線 $\textrm{OM}$ を下ろすと,$\triangle\textrm{OAM}$ が直角三角形になる
$\textrm{OA}$ は円の半径 $r$,$\textrm{OM}$ は円の中心と直線の距離$d$
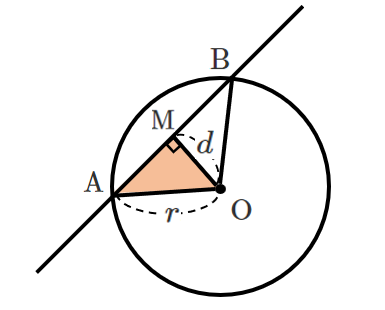
$\triangle\textrm{OAM}$ で三平方の定理を用いると $\textrm{AM}=\sqrt{r^2-d^2}$
$\textrm{AB}=2\textrm{AM}$ で弦の長さが求まる
問題
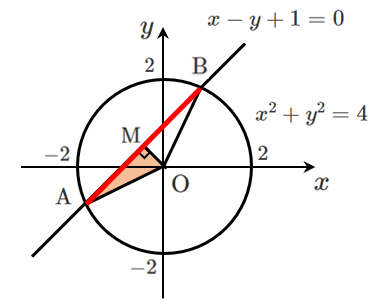
$x^2+y^2=4$ は中心が原点 $\textrm{O}$,半径が $2$ の円であるから $\textrm{OA}=2$
円の中心 $\textrm{O}$ から直線 $\textrm{AB}$ に垂線 $\textrm{OM}$ を下ろすと
$\textrm{M}$ は線分 $\textrm{AB}$ の中心であるから $\textrm{AM}=\textrm{BM}$
$\textrm{OM}$ は円の中心 $\textrm{O}$ と直線 $\textrm{AB}$ の距離より
$\displaystyle{\textrm{OM}=\frac{|0-0+1|}{\sqrt{1^2+(-1)^2}}=\frac{1}{\sqrt{2}}}$
$\triangle\textrm{OAM}$ は直角三角形であるから,三平方の定理より
$\displaystyle{\textrm{AM}=\sqrt{\textrm{OA}^2-\textrm{OM}^2}=\sqrt{2^2-\left(\frac{1}{\sqrt{2}}\right)^2}=\sqrt{\frac{7}{2}}=\frac{\sqrt{14}}{2}}$
したがって $\displaystyle{\textrm{AB}=2\textrm{AM}=\sqrt{14}}$
解と係数の関係を用いた解答
$x-y+1=0$ より $y=x+1$
これを $x^2+y^2=4$ に代入すると
$x^2+(x+1)^2=4$
$2x^2+2x-3=0$
この方程式の解は,円と直線の交点の $x$ 座標である
これらを $\alpha$,$\beta$ とすると,解と係数の関係より
$\displaystyle{\alpha+\beta=-1}$, $\displaystyle{\alpha\beta=-\frac{3}{2}}$
点 $\textrm{A}$,$\textrm{B}$ は直線 $y=x+1$ 上にあるから
$\textrm{A}(\alpha,\alpha+1)$,$\textrm{B}(\beta,\beta+1)$ である
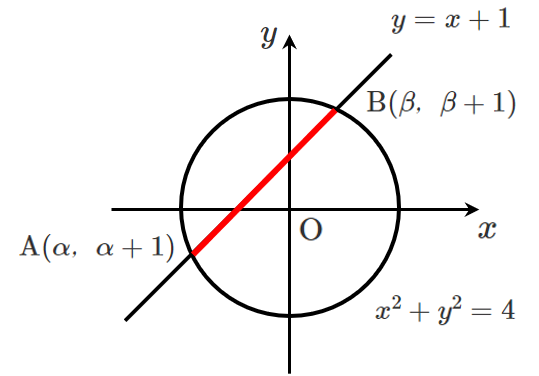
このとき
$\textrm{AB}^2=(\beta-\alpha)^2+\{(\beta+1)-(\alpha+1)\}^2$
$=2(\beta-\alpha)^2$
$=2\{(\alpha+\beta)^2-4\alpha\beta\}$
$=2\{(-1)^2-4\cdot\left(-\frac{3}{2}\right)\}$
$=14$
したがって $\textrm{AB}=\sqrt{14}$
共有点を求める方法
円と直線の共有点の座標を求め、2点間の距離で求める方法もあるが、
計算が大変なので使わないようにしましょう。
$x-y+1=0$ より $y=x+1$
これを $x^2+y^2=4$ に代入すると
$x^2+(x+1)^2=4$
$2x^2+2x-3=0$
$\displaystyle{x=\frac{-1\pm\sqrt{7}}{2}}$
$y=x+1$ に代入すると $\displaystyle{\textrm{A}\left(\frac{-1-\sqrt{7}}{2},\frac{1-\sqrt{7}}{2}\right)}$,$\displaystyle{\textrm{B}\left(\frac{-1+\sqrt{7}}{2},\frac{1+\sqrt{7}}{2}\right)}$
$\displaystyle{\textrm{AB}^2=\left(\frac{-1+\sqrt{7}}{2}-\frac{-1-\sqrt{7}}{2}\right)^2+\left(\frac{1+\sqrt{7}}{2}-\frac{1-\sqrt{7}}{2}\right)^2}$
$=(\sqrt{7})^2+(\sqrt{7})^2$
$=14$
したがって $\textrm{AB}=\sqrt{14}$




コメント