高校数学Ⅱの【図形と方程式】で学ぶ『軌跡|垂直二等分線・角の二等分線』について解説!
「軌跡が苦手」という高校生はとても多いです!
軌跡が苦手という人でも、軌跡の問題が解けるようにわかりやすく解説しました!
この投稿を見れば、軌跡の問題はバッチリ!
軌跡とは
与えられた条件を満たす点全体の集合が作る図形を、この条件を満たす点の軌跡という。
点 $\textrm{A}$ からの距離が $r$ である点 $\textrm{P}$ 全体の集合は円である
すなわち、点 $\textrm{P}$ の軌跡は、点 $\textrm{A}$ を中心とする半径 $r$ の円である
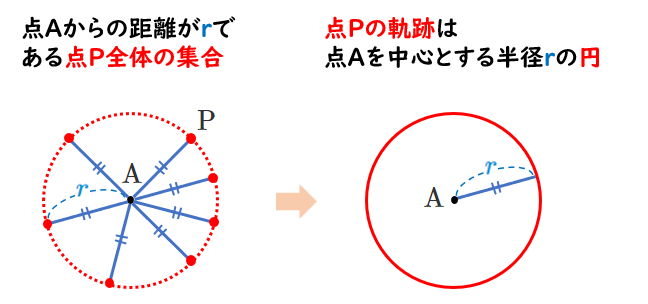
円は定点からの距離が一定であるような点の軌跡である
軌跡を求める手順
点 $\textrm{P}$ の軌跡は次の手順で求めることができる
① 軌跡を求める点 $\textrm{P}$ の座標を $(x,y)$ とおく
② 与えられた条件から,$x$,$y$ の関係式を導き,図形が何かを調べる
③ ②で求めた図形上のすべての点が,与えられた条件を満たすかどうか調べる
(明らかな場合は省略してもよい)
垂直二等分線の軌跡
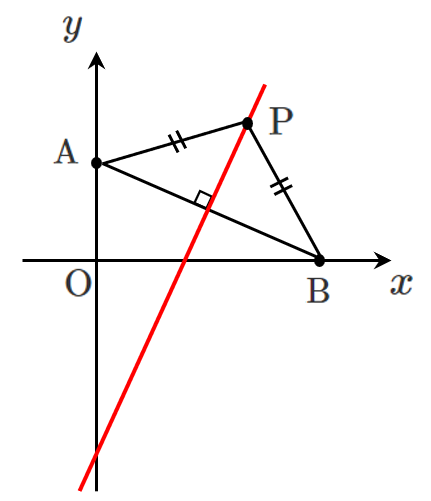
点 $\textrm{P}$ の座標を $(x,y)$ とすると
$\textrm{P}$ に関する条件は $\textrm{AP}=\textrm{BP}$ すなわち $\textrm{AP}^2=\textrm{BP}^2$
よって $x^2+(y-2)^2=(x-4)^2+y^2$
整理すると $2x-y-3=0$
したがって,点 $\textrm{P}$ の軌跡は,直線 $2x-y-3=0$ である
【補足】
・$\textrm{AP}=\textrm{BP}$ のまま用いると,$\sqrt{x^2+(y-2)^2}=\sqrt{(x-4)^2+y^2}$ となり,どうせ2乗することになるので,先に2乗 $\textrm{AP}^2=\textrm{BP}^2$ している
・求めた直線上のすべての点が,与えられた条件を満たすことが明らかなので、手順③を省略している
角の二等分線の軌跡
2直線のなす角の二等分線は、
(直線①との距離)=(直線②との距離) となる点 $\textrm{P}$ の軌跡
と考えることができる
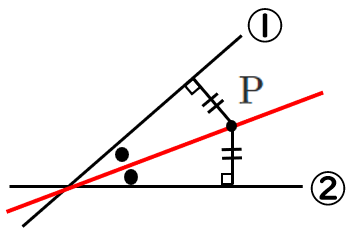
求める角の二等分線は,2直線①と②からの距離が等しい点 $\textrm{P}(X,Y)$ の軌跡なので
$\displaystyle{\frac{|X+Y-2|}{\sqrt{1^2+1^2}}=\frac{|7X-Y-2|}{\sqrt{7^2+(-1)^2}}}$
$\displaystyle{\frac{|X+Y-2|}{\sqrt{2}}=\frac{|7X-Y-2|}{5\sqrt{2}}}$
$5|X+Y-2|=|7X-Y-2|$
$\pm5(X+Y-2)=7X-Y-2$
$5(X+Y-2)=7X-Y-2$ より $X-3Y+4=0$
$-5(X+Y-2)=7X-Y-2$ より $3X+Y-3=0$
求める角の二等分線の方程式は $x-3y+4=0$,$3x+y-3=0$
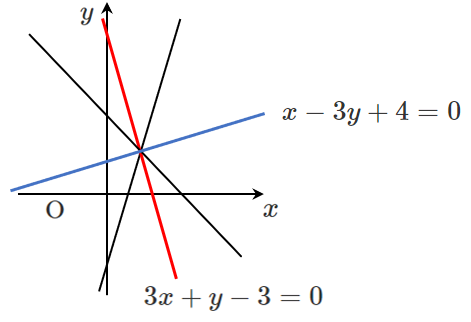
【補足】2直線の方程式に含まれている $x$,$y$ と区別するために $\textrm{P}(X,Y)$ とおいている
軌跡の方程式を答えるときは、小文字 $x$,$y$ で表す




コメント