高校数学Ⅱの【図形と方程式】で学ぶ『連動する点の軌跡』について解説!
「軌跡が苦手」という高校生はとても多いです!
軌跡が苦手という人でも、軌跡の問題が解けるようにわかりやすく解説しました!
今回は、軌跡で求める点以外に動点が与えられている問題を扱います!
この投稿を見れば、『連動する点の軌跡』はバッチリ!
解説する問題はこれです↓
軌跡とは
与えられた条件を満たす点全体の集合が作る図形を、この条件を満たす点の軌跡という。
点 $\textrm{A}$ からの距離が $r$ である点 $\textrm{P}$ 全体の集合は円である
すなわち、点 $\textrm{P}$ の軌跡は、点 $\textrm{A}$ を中心とする半径 $r$ の円である
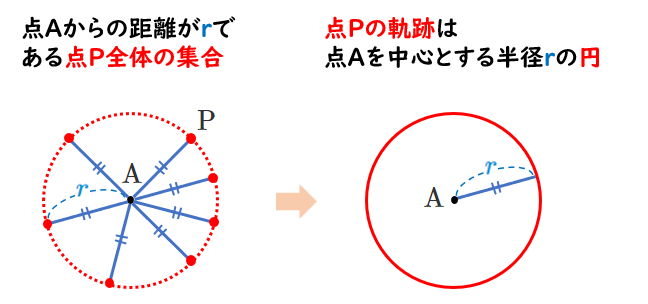
円は定点からの距離が一定であるような点の軌跡である
軌跡を求める手順
点 $\textrm{P}$ の軌跡は次の手順で求めることができる
① 軌跡を求める点 $\textrm{P}$ の座標を $(x,y)$ とおく
② 与えられた条件から,$x$,$y$ の関係式を導き,図形が何かを調べる
③ ②で求めた図形上のすべての点が,与えられた条件を満たすかどうか調べる
(明らかな場合は省略してもよい)
【補足】
方程式に含まれている $x$,$y$ と区別をするために,軌跡を求める点を $(X,Y)$ とおくこともある。その場合,軌跡の方程式を答えるときは,小文字 $x$,$y$ で表す。
連動する点の軌跡
軌跡を求める点以外に動点が与えられている場合は,その動点を $x$,$y$ 以外の文字でおく
例えば,動点を $(s,t)$ とおいた場合,関係式から $s$,$t$ を消去して $x$,$y$ の方程式を導くことで軌跡が求まる
問題
軌跡として求める点を $(X,Y)$ とおく ➡ $\textrm{P}(X,Y)$ とおく
それ以外の動点を $(s,t)$ とおく ➡ $\textrm{Q}(s,t)$ とおく
与えられた条件を $X$,$Y$,$s$,$t$ の式で表す
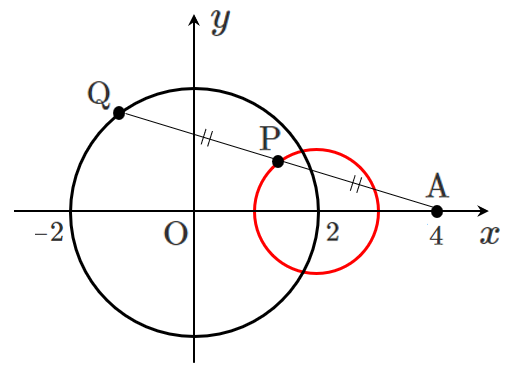
条件1:$\textrm{Q}$ が円 $x^2+y^2=4$ 上にある
条件2:$\textrm{P}(X,Y)$ は線分 $\textrm{AQ}$ の中点である
上の式から $s$,$t$ を消去して,$X$,$Y$ の式を導く
点 $\textrm{P}$,$\textrm{Q}$ の座標をそれぞれ $(X,Y)$,$(s,t)$ とする
$\textrm{Q}$ は円 $x^2+y^2=4$ 上にあるので $s^2+t^2=4$ … ①
また,$\textrm{P}$ は線分 $\textrm{AQ}$ の中点なので $\displaystyle{X=\frac{s+4}{2}}$,$\displaystyle{Y=\frac{t}{2}}$
すなわち $s=2X-4$,$t=2Y$
これらを①に代入すると $(2X-4)^2+(2Y)^2=4$
$\{2(X-2)\}^2+(2Y)^2=4$
$4(X-2)^2+4Y^2=4$
$(X-2)^2+Y^2=1$
求める点 $\textrm{P}$ の軌跡は 円 $(x-2)^2+y^2=1$
したがって,中心 $(2,0)$,半径 $1$ の円




コメント