高校数学Ⅱ『図形と方程式』で学ぶ『積の形で与えられた不等式の表す領域』について解説!
積の形で与えられた不等式の領域を図示するために必要な考え方をまとめました!
この投稿を見れば、不等式の領域の問題はバッチリ!
この投稿で扱う問題はこれ↓
(1) $(x+y-2)(x-y)>0$
(2) $(x^2+y^2-4)(x+y-1)≦0$
積の形で与えられた不等式の領域の考え方
不等式 $AB>0$ または $AB<0$ で表された不等式の領域は、
2つの連立不等式に分けて考える

問題
(1) $(x+y-2)(x-y)>0$
(2) $(x^2+y^2-4)(x+y-1)≦0$
(1) $(x+y-2)(x-y)>0$ より
\begin{align} \left\{ \begin{array}{ll} x+y-2>0 \\ x-y>0 \end{array} \right. \cdots① または \left\{ \begin{array}{ll} x+y-2<0 \\ x-y<0 \end{array} \right. \cdots②\end{align}
すなわち
\begin{align} \left\{ \begin{array}{ll} y>-x+2 \\ y>x \end{array} \right. \cdots ① または \left\{ \begin{array}{ll} y<-x+2 \\ y<x \end{array} \right. \cdots②\end{align}
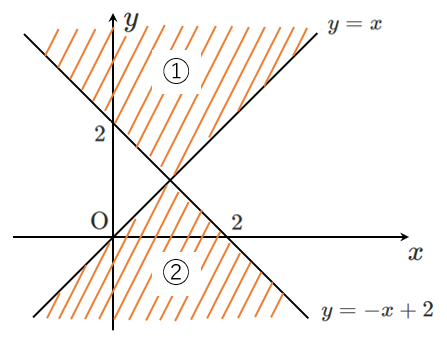
領域①は、直線 $y=-x+2$ の上側 かつ 直線 $y=x$ の上側
領域②は、直線 $y=-x+2$ の下側 かつ 直線 $y=x$ の下側
よって、求める領域は、①と②の表す領域を合わせたものであるから、下図の斜線部分である
ただし、境界線は含まない
(2) $(x^2+y^2-4)(x+y-1)≦0$ より
\begin{align} \left\{ \begin{array}{ll} x^2+y^2-4≧0 \\ x+y-1≦0 \end{array} \right. \cdots① または \left\{ \begin{array}{ll} x^2+y^2-4≦0 \\ x+y-1≧0 \end{array} \right. \cdots②\end{align}
すなわち
\begin{align} \left\{ \begin{array}{ll} x^2+y^2≧4 \\ y≦-x+1 \end{array} \right. \cdots① または \left\{ \begin{array}{ll} x^2+y^2≦4 \\ y≧-x+1 \end{array} \right. \cdots②\end{align}
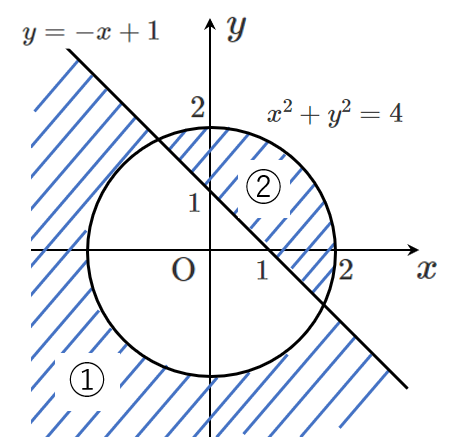
領域①は、円 $x^2+y^2=4$ の外側 かつ 直線 $y=-x+1$ の下側
領域②は、円 $x^2+y^2=4$ の内側 かつ 直線 $y=-x+1$ の上側
よって、求める領域は、①と②の表す領域を合わせたものであるから、下図の斜線部分である
ただし、境界線は含む




コメント