高校数学Ⅱの【図形と方程式】で学ぶ『軌跡|垂直二等分線・角の二等分線』について解説!
「軌跡が苦手」という高校生はとても多いです!
軌跡が苦手という人でも、軌跡の問題が解けるようにわかりやすく解説しました!
この投稿を見れば、軌跡の問題はバッチリ!
軌跡とは
与えられた条件を満たす点全体の集合が作る図形を、この条件を満たす点の軌跡という。
点 $\textrm{A}$ からの距離が $r$ である点 $\textrm{P}$ 全体の集合は円である
すなわち、点 $\textrm{P}$ の軌跡は、点 $\textrm{A}$ を中心とする半径 $r$ の円である
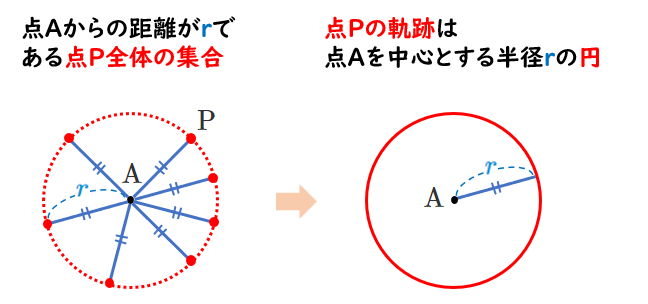
円は定点からの距離が一定であるような点の軌跡である
軌跡を求める手順
点 $\textrm{P}$ の軌跡は次の手順で求めることができる
① 軌跡を求める点 $\textrm{P}$ の座標を $(x,y)$ とおく
② 与えられた条件から,$x$,$y$ の関係式を導き,図形が何かを調べる
③ ②で求めた図形上のすべての点が,与えられた条件を満たすかどうか調べる
(明らかな場合は省略してもよい)
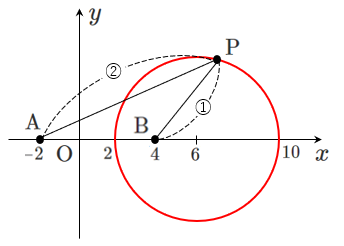
2定点に対して比で表される点の軌跡
点 $\textrm{P}$ の座標を $(x,y)$ とすると
$\textrm{AP}:\textrm{BP}=2:1$ より $\textrm{AP}=2\textrm{BP}$
両辺を2乗して $\textrm{AP}^2=4\textrm{BP}^2$
$(x+2)^2+y^2=4\{(x-4)^2+y^2\}$
$3x^2+3y^2-36x+60=0$
$x^2+y^2-12x+20=0$
$(x-6)^2+y^2=16$ … ① ←どのような図形かわかる式まで変形
よって,与えられた条件を満たす点 $\textrm{P}$ は①上にある
逆に,①上のすべての点は与えられた条件を満たす
したがって,点 $\textrm{P}$ の軌跡は,中心 $(6,0)$,半径 $4$ の円
【補足】
・$\textrm{AP}=2\textrm{BP}$ のまま用いると,$\sqrt{(x+2)^2+y^2}=\sqrt{(x-4)^2+y^2}$ となり,どうせ2乗することになるので,先に2乗 $\textrm{AP}^2=4\textrm{BP}^2$ している
・円の場合,方程式ではなく,図形の説明をする
「円 $(x-6)^2+y^2=16$ 」ではなく,「中心 $(6,0)$,半径 $4$ の円」と答える
アポロニウスの円
$m>0$,$n>0$ のとき,平面上の2点 $\textrm{A}$,$\textrm{B}$ に対して,$\textrm{AP}:\textrm{BP}=m:n$ を満たす点 $\textrm{P}$ の軌跡は
(ア) $m≠n$ のとき
線分 $\textrm{AB}$ を $m:n$ に内分する点と外分する点を
直径の両端とする円(アポロニウスの円)
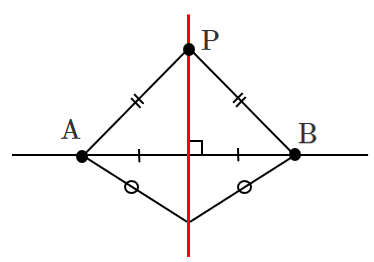
(イ) $m=n$ のとき
線分 $\textrm{AB}$ の垂直二等分線
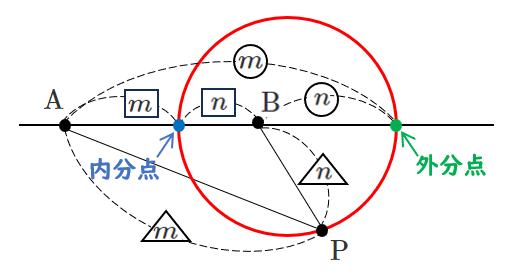
アポロニウスの円を利用すると,簡単に軌跡が求まる
条件より,この図形はアポロニウスの円を表す
線分 $textrm{AB}$ を $2:1$ に内分する点は $(2,0)$
線分 $textrm{AB}$ を $2:1$ に外分する点は $(10,0)$
2点 $(2,0)$,$(10,0)$ を結ぶ線分の中点が円の中心だから,
円の中心は $(6,0)$
また,円の半径は $4$
したがって,求める軌跡は 中心 $(6,0)$,半径 $4$ の円




コメント