集合と要素について,よくある悩みが
⊂の向きがわからない
⊂と∈の違いがわからない
です!
わかってしまえば,「それだけのことか」と感じるくらい簡単です!
この投稿を見たら,あなたの悩みも一瞬で解決します!
集合と要素
集合…範囲がはっきりしたものの集まり
要素…集合を構成しているひとつひとつ
例 $5$ 以下の自然数全体の集合 $A$
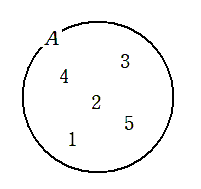
$A$ の要素は $1,2,3,4,5$
集合 $A$ を以下のように表す
$A=\{1,2,3,4,5\}$
$\{ \}$ の中に要素を書くと,その要素が集まった集合を表す
部分集合
$A$ のすべての要素が $B$ の要素でもあるとき、以下のようになる
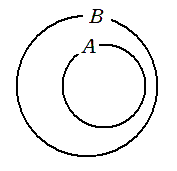
このとき
$A$ を $B$ の部分集合
$A$ は $B$ に含まれる
$B$ は $A$ を含む
という
記号を用いて表すと
$A⊂B$ または $B⊃A$
となる
⊂ と ⊃ の使い分け

$⊃$ と $⊂$ のどっちを使ったらいいか分からなくなる…

「不等号と同じ」と考えよう!
不等号を使うときは「大きい方に開く」が鉄則
$3<4,4>3$ のように $4$ の方が大きいので $4$ の方に開く
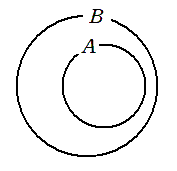
集合も同様に,$B$ の集合の方が大きいので
$A⊂B$ または $B⊃A$
のように,$B$ の方に開く
集合と要素を記号で表す
例 $5$ 以下の自然数全体の集合 $A$
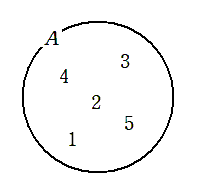
$1$ は集合 $A$ の要素であるといい,記号で表すと
$1∈A$
要素である $1$ より 集合 $A$ の方が大きいので
集合 $A$ の方に開く
$要素∈集合$
⊂ と ∈ の違い

$⊂$ と $∈$ の違いをきちんと理解しておこう!
集合同士の関係を表す記号が $⊂$ と $⊃$
$集合⊂集合$
要素と集合の関係を表す記号が $∈$ と $∋$
$要素∈集合$
まとめ
集合…範囲がはっきりしたものの集まり
要素…集合を構成しているひとつひとつ
$\{ \}$ の中に要素を書くと、その要素が集まった集合を表す
集合同士の関係を表す記号が $⊂$ と $⊃$
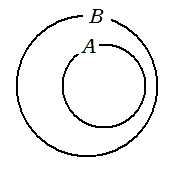
$A⊂B$ または $B⊃A$
大きい集合の方に開く
要素と集合の関係を表す記号が $∈$ と $∋$
$要素∈集合$
例 $1$ は集合 $A$ の要素 $1∈A$
問題
$6$ の正の約数全体の集合を $A$,$12$ の正の約数全体の集合を $B$,
$3$ 以下の自然数全体の集合を $C$ とする。次の空欄に入る記号を選べ。
$「⊂」$ $「⊃」$ $「∈」$ $「∋」$
(1) $A$ □ $B$
(2) $A$ □ $C$
(3) $6$ □ $A$
(4) $\{1\}$ □ $C$
解答
集合 $A$,$B$,$C$ を図で表すと以下のようになる
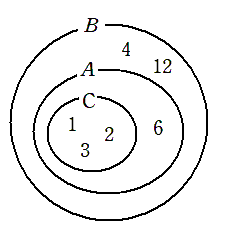
(1) $A$ □ $B$
$A$ は $B$ に含まれるので $A⊂B$
$B$ の集合の方が大きいので $B$ の方に開く
(2) $A$ □ $C$
$A$ は $C$ を含むので $A⊃C$
$A$ の集合の方が大きいので $A$ の方に開く
(3) $6$ □ $A$
$6$ は $A$ の要素なので $6∈A$
集合と要素の関係なので $∈$ または $∋$ を使う
$要素∈集合$
(4) ${1}$ □ $C$
$\{1\}$ は 要素 $1$ を含む集合を表す
集合 $\{1\}$ は $C$ に含まれるので ${1}⊂C$
集合同士の関係なので $⊂$ または $⊃$ を使う

$⊂$ と $∈$ の違いをきちんと理解しよう!
🔰基本…まずはこの記事から!
🔵標準…基本問題や公式の理解度が重要!
🔴応用…場合分けなど思考力が要求される!




コメント