高校数学Ⅱの【三角関数】で学ぶ『三角関数の最大・最小(sinθ+cosθ)』について解説!
三角関数の最大・最小に関する問題は,模試でも頻出の重要問題!
この投稿を見て,確実に解けるように練習しよう!
問題
問題
$0≦\theta≦\pi$ とする。$y=\sin2\theta+2\sin\theta+2\cos\theta$ について次の問いに答えよ。
(1) $\sin\theta+\cos\theta=t$ とおいて,$y$ を $t$ の関数で表せ。
(2) $t$ のとりうる値の範囲を求めよ。
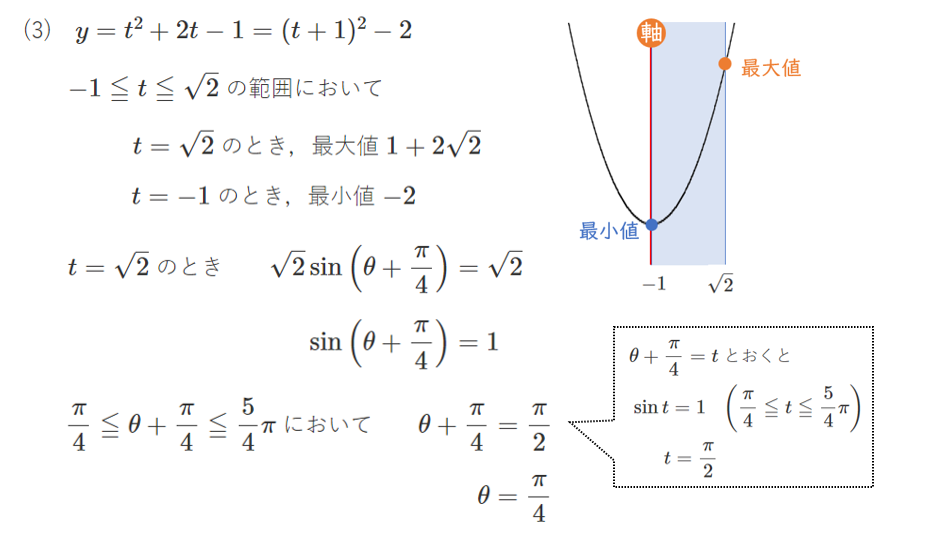
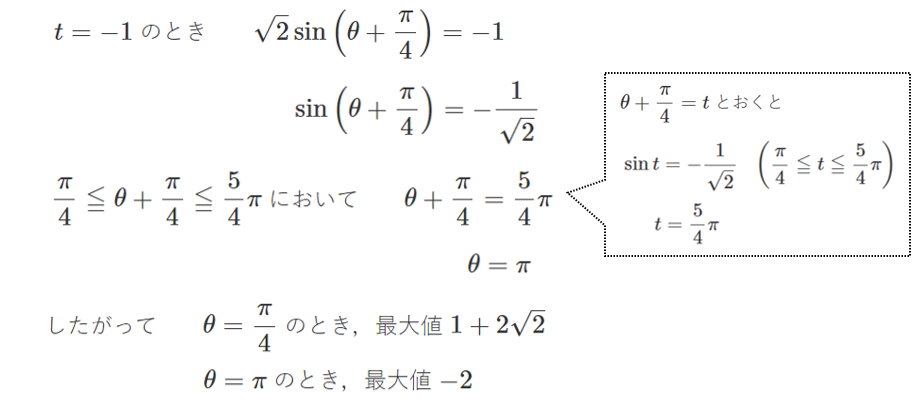
(3) $y$ の最大値,最小値と,そのときの $\theta$ の値を求めよ。
(1) $\sin\theta+\cos\theta=t$ とおいて,$y$ を $t$ の関数で表せ。
(2) $t$ のとりうる値の範囲を求めよ。
(3) $y$ の最大値,最小値と,そのときの $\theta$ の値を求めよ。
解答






コメント