
「確率の加法定理」とは確率の足し算のこと!
どういうときに確率の足し算を使うか学ぼう!
互いに排反
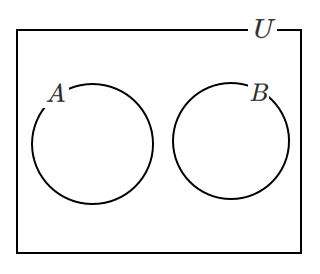

「互いに排反」は「同時に起こらない」と覚えておこう!
「偶数を引く」という事象 $A$
「3の倍数を引く」という事象を $B$
「5の倍数を引く」という事象を $C$
とするとき,どの事象とどの事象が互いに排反か。
事象 $A$ は $2,4,6,8,10$ を引く
事象 $B$ は $3,6,9$ を引く
事象 $C$ は $5,10$ を引く
互いに排反な(同時に起こらない)のは
事象 $B$ と事象 $C$
確率の加法定理
$(AまたはBの確率)=(Aの確率)+(Bの確率)$
3つ以上でも同様

「互いに排反」(同時に起こらない)なら足せる
と覚えておこう!
1等が $2$ 枚,2等が $3$ 枚,3等が $15$ 枚
入っているとき,1等から3等までのいずれかが当たる確率
1等が当たる確率 $\displaystyle{\frac{2}{100}}$
2等が当たる確率 $\displaystyle{\frac{3}{100}}$
3等が当たる確率 $\displaystyle{\frac{15}{100}}$
各等が当たる事象は互いに排反なので
(同時に起こらない)
$\displaystyle{\frac{2}{100}+\frac{3}{100}+\frac{15}{100}}$
$\displaystyle{=\frac{20}{100}}$
$\displaystyle{=\frac{1}{5}}$
まとめ
● $A$ と $B$ が互いに排反
$A$ と $B$ が同時に起こらない
● 確率の加法定理
$A$ と $B$ が互いに排反ならば
$(AまたはBの確率)=(Aの確率)+(Bの確率)$
3つ以上でも同様
問題
(1) さいころを2個投げるとき,目の和が5の倍数
(2) 赤玉3個と白玉4個入った袋から同時に2個玉を取り出すとき,2個が同じ色
(1) さいころを2個投げるとき,目の和が5の倍数
[1] 目の和が $5$ のとき
目の出方が $(1,4)$,$(2,3)$,$(3,2)$,$(4,1)$
目の和が $5$ になる確率は $\displaystyle{\frac{4}{36}}$
[2] 目の和が $10$ のとき
目の出方が $(4,6)$,$(5,5)$,$(6,4)$
目の和が $10$ になる確率は $\displaystyle{\frac{3}{36}}$
[1] と [2] は互いに排反なので
$\displaystyle{\frac{4}{36}+\frac{3}{36}}$
$\displaystyle{=\frac{7}{36}}$
(2) 赤玉3個と白玉4個入った袋から同時に2個玉を取り出すとき,2個が同じ色
[1] 2個とも赤玉のとき
$\displaystyle{\frac{_3C_2}{_7C_2}=\frac{3}{21}}$
[2] 2個とも白玉のとき
$\displaystyle{\frac{_4C_2}{_7C_2}=\frac{6}{21}}$
[1] と [2] は互いに排反なので
$\displaystyle{\frac{3}{21}+\frac{6}{21}}$
$\displaystyle{=\frac{9}{21}}$
$\displaystyle{=\frac{3}{7}}$
$_nC_r$ を使った確率の復習はこれ↓


同時に起こらないことは足せる!
しっかりおさえておこう!




コメント