
頻出の「チェバの定理」について学ぼう!
チェバの定理
$\triangle ABC$ の内部に点 $O$ をとり,頂点 $A$,$B$,$C$ と点 $O$ を結ぶ直線が向かい合う辺と,それぞれ $P$,$Q$,$R$ で交わるとき
$\displaystyle{\frac{BP}{PC}・\frac{CQ}{QA}・\frac{AR}{RB}=1}$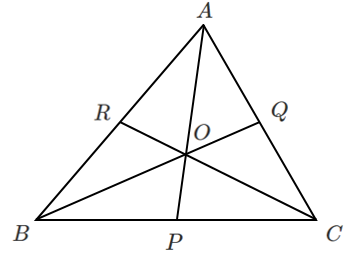

どこかの頂点から始めて一筆書きで一周すれば,式が作れるよ!
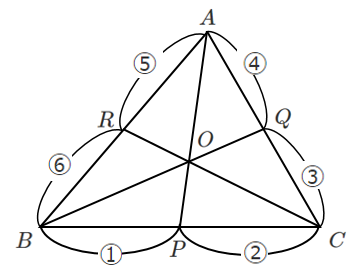
点 $B$ から始める
$\displaystyle{\frac{①}{②}・\frac{③}{④}・\frac{⑤}{⑥}=1}$
点 $C$ から始める
$\displaystyle{\frac{③}{④}・\frac{⑤}{⑥}・\frac{①}{②}=1}$
点 $A$ から始める
$\displaystyle{\frac{⑤}{⑥}・\frac{①}{②}・\frac{③}{④}=1}$
時計回りに回ってもよい
証明

チェバの定理の証明の前に準備をしよう!
証明の準備
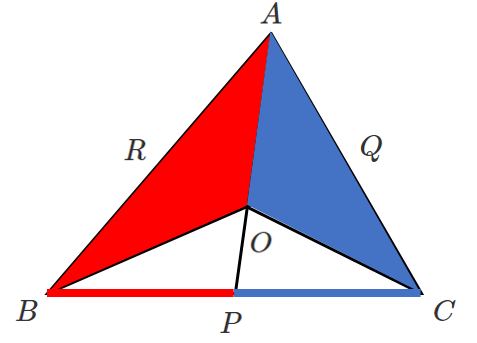
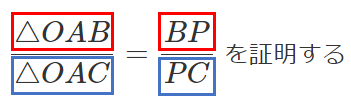
[証明]
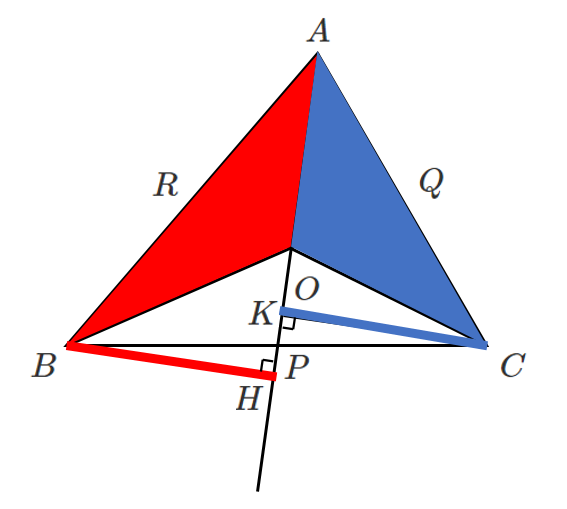
上図のように
$\triangle OAB$ の辺 $OA$ を底辺としたときの高さ $BH$
$\triangle OAC$ の辺 $OA$ を底辺としたときの高さ $CK$ をとる
底辺 $OA$ は等しいので,$\triangle OAB$ と $\triangle OAC$ の面積比は高さの比と等しい
$\triangle OAB:\triangle OAC=BH:CK$
$BK/\!/CH$ より $BH:CK=BP:PC$
よって $\triangle OAB:\triangle OAC=BH:CK$
$\triangle OAB\times CK=\triangle OAC\times BH$
すなわち $\displaystyle{\frac{\triangle OAB}{\triangle OAC}=\frac{BP}{PC}}$
チェバの定理の証明
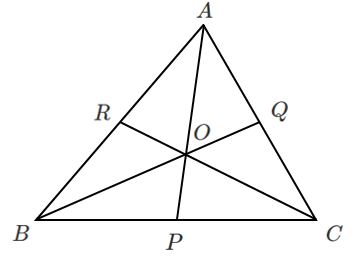
$\displaystyle{\frac{BP}{PC}・\frac{CQ}{QA}・\frac{AR}{RB}=1}$ を証明する
[証明]
$\displaystyle{\frac{BP}{PC}=\frac{\triangle OAB}{\triangle OAC}}$
$\displaystyle{\frac{CQ}{QA}=\frac{\triangle OBC}{\triangle OAB}}$
$\displaystyle{\frac{AR}{RB}=\frac{\triangle OAC}{\triangle OBC}}$
よって
$\displaystyle{\frac{BP}{PC}・\frac{CQ}{QA}・\frac{AR}{RB}=\frac{\triangle OAB}{\triangle OAC}・\frac{\triangle OBC}{\triangle OAB}・\frac{\triangle OAC}{\triangle OBC}=1}$

チェバの定理は面積比を使って証明できる!
まとめ
● チェバの定理
$\displaystyle{\frac{BP}{PC}・\frac{CQ}{QA}・\frac{AR}{RB}=1}$
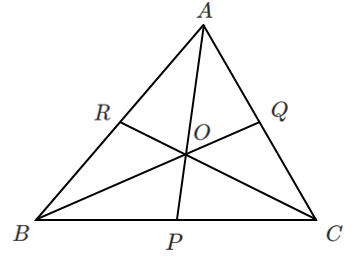
どこかの頂点から一筆書きで一周する
問題
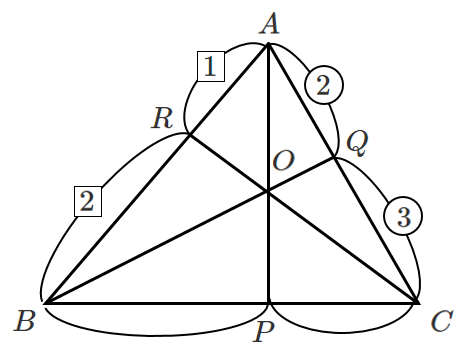
チェバの定理より
$\displaystyle{\frac{BP}{PC}・\frac{3}{2}・\frac{1}{2}=1}$
$\displaystyle{\frac{BP}{PC}・\frac{3}{4}=1}$
$\displaystyle{\frac{BP}{PC}=\frac{4}{3}}$
よって $BP:PC=4:3$

一筆書きで一周したら簡単に式が作れるね!




コメント