最大公約数
約数
$24$ の正の約数
$1,2,3,4,6,8,12,24$
$24$ を割り切ることができる数
公約数

公約数とは共通する約数のこと!
$24$ と $36$ の正の公約数
$24$ の約数
$1,2,3,4,6,8,12,24$
$36$ の約数
$1,2,3,4,6,9,12,18,36$
公約数は
$1,2,3,4,6,12$
最大公約数

最大公約数は公約数の中で最大のもの!
$24$ と $36$ の正の公約数は
$1,2,3,4,6,12$
$24$ と $36$ の最大公約数は $12$

約数→公約数→最大公約数の順に理解しておこう!
最小公倍数
倍数
$12$ の正の倍数
$12,24,36,48,60,72,84,\cdots$
$12$ を整数倍したもの
公倍数

公倍数とは共通する倍数のこと!
$12$ と $16$ の正の公倍数
$12$ の約数
$12,24,36,48,60,72,84,96,\cdots$
$16$ の約数
$16,32,48,64,80,96,112,128,\cdots$
公倍数は
$48,96,144,\cdots$
最小公倍数

最小公倍数は公倍数の中で最小のもの!
$12$ と $16$ の正の公倍数は
$48,96,144,\cdots$
$12$ と $16$ の最大公約数は $48$

倍数→公倍数→最小公倍数の順に理解しておこう!
最大公約数と最小公倍数の求め方

最小公倍数と最小公倍数を簡単に求める方法を学ぼう!
2つの場合
最大公約数と最小公倍数を求めたい数を並べる
素数で割っていく
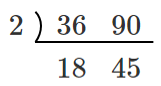
素数で割れなくなったら終了
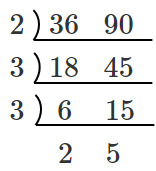
最大公約数は左 $2・3・3=18$
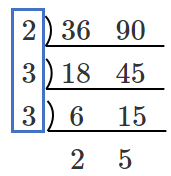
最小公倍数は $L$ 字 $2・3・3・2・5=180$


素因数分解みたいな方法で求まるね!
3つの場合

3つの場合は,最大公約数と最小公倍数を分けて考えるのがポイント!
○最大公約数
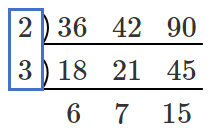
最大公約数は $2・3=6$
○最小公倍数
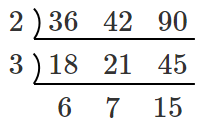
$6$ と $7$ と $15$ について
$6$ と $15$ は $3$ で割れるので
$7$ を無視して割る
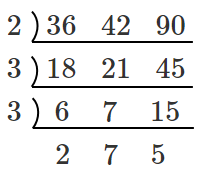
ここまでして最小公倍数を計算する

最小公倍数は $2・3・3・2・7・5=1260$

3つ以上の場合は注意が必要だね!
まとめ
● 最大公約数
公約数(共通する約数)の中で最大のもの
● 最小公倍数
公倍数(共通する倍数)の中で最小のもの
● 最大公約数と最小公倍数の求め方
素因数分解のように割っていく
問題
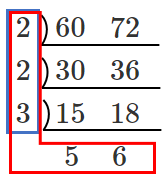
最大公約数は $2・2・3=12$
最小公倍数は $2・2・3・5・6=360$
〇最大公約数
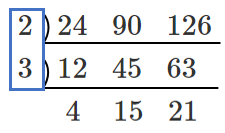
最大公約数は $2・3=6$
〇最小公倍数

最小公倍数は $2・3・3・4・5・7=2520$

最大公約数と最小公倍数を求めるだけなら,この方法がいいね!




コメント