
$10$ 進法を $n$ 進法で表す方法を学ぼう!
$n$ 進法を $10$ 進法で表す方法はこれ↓

10 進法
$10$ 進法は位取りが $10^○$ なので,
$10$ で割っていくと,余りの部分に各位の数が出てくる
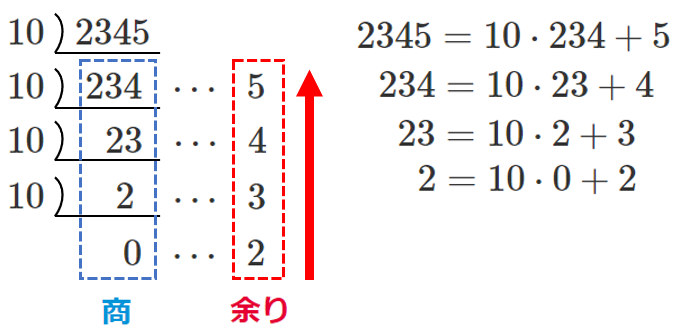
余りを下から順番に並べると $2345$ になる

これを用いると,$n$ 進法を $10$ 進法で表すことができる!
2 進法を 10 進法で表す

$2$ 進法を $10$ 進法で表してみよう!
$2$ 進法は位取りが $2^○$ なので,
$2$ で割っていくと,余りの部分に各位の数が出てくる

よって, $22=10110_{(2)}$

$10$ 進法を $2$ 進法で表すときは,割る数を $2$ として割り算を繰り返して,余りを下から順番に並べる!
3 進法を 10 進法で表す

$3$ 進法を $10$ 進法で表してみよう!
$3$ 進法は位取りが $3^○$ なので,
$3$ で割っていくと,余りの部分に各位の数が出てくる
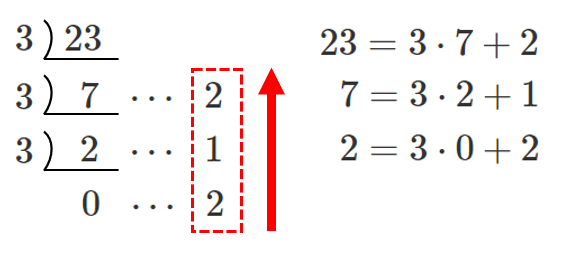
よって, $23=212_{(3)}$

$10$ 進法を $3$ 進法で表すときは,割る数を $3$ として割り算を繰り返して,余りを下から順番に並べる!
10 進法を n 進法で表す
$2$ 進法,$3$ 進法と同様にして,
$10$ 進法を $4$ 進法で表すときは
割る数を $4$ として割り算を繰り返して,余りを下から順に並べる
$10$ 進法を $5$ 進法で表すときは
割る数を $5$ として割り算を繰り返して,余りを下から順に並べる
というように,
$10$ 進法を $n$ 進法で表すときは
割る数を $n$ として割り算を繰り返して,余りを下から順に並べる
まとめ
● $10$ 進法を $2$ 進法で表す
割る数を $2$ として割り算を繰り返して,余りを下から順に並べる
● $10$ 進法を $3$ 進法で表す
割る数を $3$ として割り算を繰り返して,余りを下から順に並べる
● $10$ 進法を $n$ 進法で表す
割る数を $n$ として割り算を繰り返して,余りを下から順に並べる
問題
(2) $29$ を $3$ 進法で表せ。
(3) $29$ を $4$ 進法で表せ。
(1) $29$ を $2$ 進法で表せ。
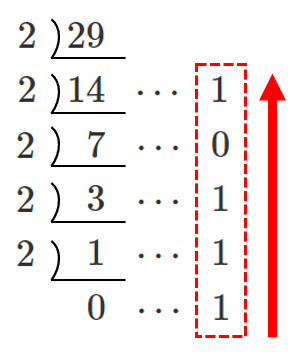
$29=11101_{(2)}$
(2) $29$ を $3$ 進法で表せ。
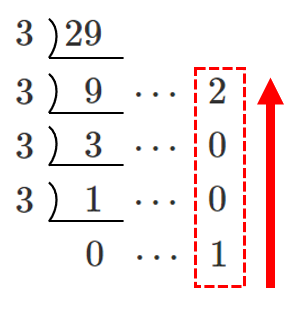
$29=1002_{(3)}$
(3) $29$ を $4$ 進法で表せ。
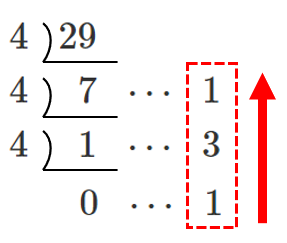
$29=131_{(4)}$

これで $10$ 進法は $n$ 進法で表すことができるね!




コメント