高校数学Ⅱで学ぶ『2次方程式の決定』に関する問題をわかりやすく解説!
この投稿では、解から2次方程式を求める方法を学びます!
「解と係数の関係」を絡めた頻出の問題も解説します!
2次方程式の決定
2数 $\alpha$,$\beta$ を解とする2次方程式の1つは
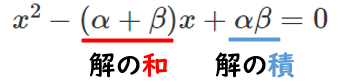
➡解の和と積で、2次方程式が求まる
例えば、「$x=2,3$ を解にもつような2次方程式」は、以下のように2次方程式を解く手順と逆の計算で求まる。
$x=2,3$
$(x-2)(x-3)=0$
$x^2-5x+6=0$
$x=2,3$ を解にもつ2次方程式は $x^2-5x+6=0$ である
これと同様にして、「2数 $\alpha$,$\beta$ を解にもつような2次方程式」は
$x=\alpha$,$\beta$
$(x-\alpha)(x-\beta)=0$
$x-(\alpha+\beta)x+\alpha\beta=0$
2数 $x=\alpha$,$\beta$ を解にもつ2次方程式の1つは $x^2-(\alpha+\beta)x+\alpha\beta=0$ である
【注意】
厳密には「$x=2,3$ を解にもつ2次方程式は $x^2-5x+6=0$」 ではなく、
「$x=2,3$ を解にもつ2次方程式の1つは $x^2-5x+6=0$」である
$x^2-5x+6=0$ の両辺を2倍した方程式 $2x^2-10x+12=0$ も $x=2,3$ を解にもつので
(両辺を3倍、4倍、…した方程式も)
$x=2,3$ を解にもつ2次方程式は無数に存在する
解から2次方程式を求める問題
解の和は $(2-i)+(2+i)=4$
解の積は $(2-i)(2+i)=2^2-i^2=5$
求める2次方程式は $x^2-4x+5=0$ ← $x^2-($解の和$)x+($解の積$)=0$
和と積が与えられている2数を求める
求める2数は,和が $3$,積が $3$ なので,
2次方程式 $x^2-3x+3=0$ の解である ← $x^2-($解の和$)x+($解の積$)=0$
この方程式を解くと $\displaystyle{x=\frac{3\pm\sqrt{3}i}{2}}$
求める2数は $\displaystyle{\frac{3+\sqrt{3}i}{2}}$ と $\displaystyle{\frac{3-\sqrt{3}i}{2}}$
【検算】
和は $\displaystyle{\frac{3+\sqrt{3}i}{2}+\frac{3-\sqrt{3}i}{2}=\frac{6}{2}=3}$
積は $\displaystyle{\frac{3+\sqrt{3}i}{2}\times\frac{3-\sqrt{3}i}{2}=\frac{9+3}{4}=3}$
解と係数の関係を利用する問題
解と係数の関係より $\alpha+\beta=3$,$\alpha\beta=5$
求める2次方程式の解は $\displaystyle{\frac{1}{\alpha}}$,$\displaystyle{\frac{1}{\beta}}$ なので,
解の和は $\displaystyle{\frac{1}{\alpha}+\frac{1}{\beta}=\frac{\alpha+\beta}{\alpha\beta}=\frac{3}{5}}$
解の積は $\displaystyle{\frac{1}{\alpha}\times\frac{1}{\beta}=\frac{1}{\alpha\beta}=\frac{1}{5}}$
求める2次方程式は $\displaystyle{x^2-\frac{3}{5}x+\frac{1}{5}=0}$ ← $x^2-($解の和$)x+($解の積$)=0$
両辺 $5$ 倍して $5x^2-3x+1=0$

2次方程式の決定をするときは,
$x^2-(解の和)x+(解の積)=0$
を使おう!
「解と係数の関係」に自信がなかったらこれ↓





コメント