高校数学Ⅱで学ぶ『剰余の定理』について解説しました!
『剰余の定理』を使えば、整式を1次式で割った余りを簡単に求めることができます!
この投稿を読めば、『剰余の定理』の使い方が理解できます!
剰余の定理
【証明】
$P(x)$ を $x-k$ で割ったときの商を $Q(x)$,余りを $R$ とすると,
$P(x)=(x-k)Q(x)+R$ ← (割られる式)=(割る式)×(商)+(余り)
$x=k$ を代入すると $P(k)=R$
つまり, $P(k)$ は $P(x)$ を $x-k$ で割った余り $R$ と等しい
整式を1次式 $x-k$ で割った余り
(2) $x^3-x^2-3x+2$ を $x+1$ で割った余りを求めよ。
(1) $P(x)=x^3-3x^2+x-2$ とする
剰余の定理より,$P(x)$ を $x-1$ で割った余りは $P(1)$ と等しい
$P(1)=1^3-3\cdot1^2+1-2=-3$
よって,余りは $-3$
(2) $P(x)=x^3-x^2-3x+2$ とする
剰余の定理より,$P(x)$ を $x+1$ で割った余りは $P(-1)$ と等しい
$P(-1)=(-1)^3-(-1)^2-3\cdot(-1)+2=3$
よって,余りは $3$
剰余の定理を用いれば、整式を1次式で割った余りを筆算を使わずに求めることができる。
ちなみに、筆算を使っても答えは一致する。
(1)
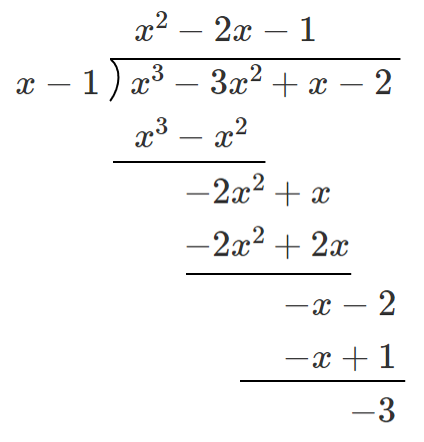
整式を1次式 $ax+b$ で割った余り
【証明】
$P(x)$ を $ax+b$ で割ったときの商を $Q(x)$,余りを $R$ とすると,
$P(x)=(ax+b)Q(x)+R$ ← (割られる式)=(割る式)×(商)+(余り)
$\displaystyle{x=-\frac{b}{a}}$ を代入すると $\displaystyle{P\left(-\frac{b}{a}\right)=R}$
つまり, $\displaystyle{P\left(-\frac{b}{a}\right)}$ は $P(x)$ を $ax+b$ で割った余り $R$ と等しい
$P(x)=x^3-3x^2+x-2$ とすると,剰余の定理より
$P(x)$ を $2x+1$ で割った余りは $\displaystyle{P\left(-\frac{1}{2}\right)}$ と等しい
$\displaystyle{P\left(-\frac{1}{2}\right)=\left(-\frac{1}{2}\right)^3-3\cdot\left(-\frac{1}{2}\right)^2+\left(-\frac{1}{2}\right)-2=-\frac{27}{8}}$
よって,余りは $\displaystyle{-\frac{27}{8}}$
剰余の定理を利用する問題
$P(x)=2x^3-x^2-3x+a$ とする
剰余の定理より,$P(x)$ を $x+1$ で割った余りは $P(-1)$ と等しく
その余りが $1$ なので $P(-1)=1$
これを計算すると $2\cdot(-1)^3-(-1)^2-3\cdot(-1)+a=1$
したがって $a=1$




コメント