高校数学Ⅱで学ぶ『内分点・外分点の座標』について解説しました!
忘れやすい公式の1つである『内分点・外分点の公式』を覚えやすく説明しています!
ポイントは、「内分は足してクロス」「外分は引いてクロス」
この投稿を見れば、『内分点・外分点の座標』はバッチリ!

内分点と外分点の座標を求める方法について学ぼう!
内分点と外分点とは
● 線分 $\textrm{AB}$ の内分点と外分点の位置

● 内分点
線分 $\textrm{AB}$ を $m:n$ に内分する点 $\textrm{P}$

点 $\textrm{P}$ は $\textrm{AP}:\textrm{PB}=m:n$ を満たす
$\textrm{AB}$ を分ける点なので,$\textrm{P}$ を $\textrm{AB}$ の間に入れる
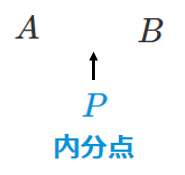
$\textrm{A}→\textrm{P}→\textrm{B}$ の一筆書きで $m:n$
$\textrm{A}$$\textrm{P}$$:$$\textrm{P}$$\textrm{B}=m:n$
● 外分点
線分 $\textrm{AB}$ を $m:n$ に外分する点 $\textrm{Q}$
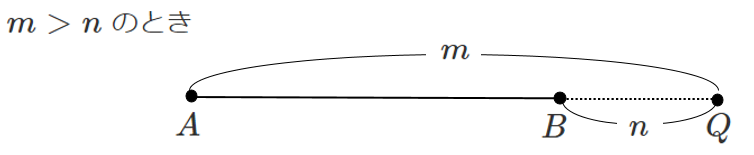
点 $\textrm{Q}$ は $\textrm{AQ}:\textrm{QB}=m:n$ を満たす
$\textrm{AB}$ を分ける点なので,$\textrm{Q}$ を $\textrm{AB}$ の間に入れる
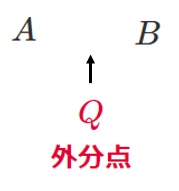
$\textrm{A}→\textrm{Q}→\textrm{B}$ の一筆書きで $m:n$
$\textrm{A}$$\textrm{Q}$$:$$\textrm{Q}$$\textrm{B}=m:n$
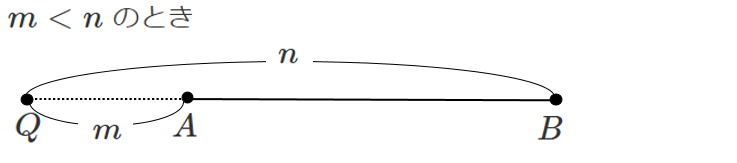
外分点は $m$ と $n$ の大小関係によって
$\textrm{A}$ 側にとるか,$\textrm{B}$ 側にとるかが変わるので注意
内分点と外分点の復習はこれ↓

数直線における内分点・外分点

平面上の内分点・外分点の座標を考える前に,数直線上の内分点・外分点の座標を求める方法を学ぼう!
数直線上の点の表し方
数直線上において,点 $\textrm{P}$ の座標が $a$ であるとき,
点 $\textrm{P}(a)$ と表す
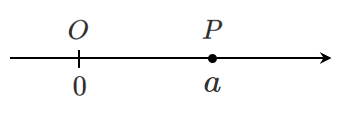
例えば,$\textrm{P}(1)$,$\textrm{Q}(3)$の場合
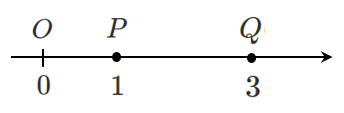
数直線上の2点間の距離
2点 $\textrm{P}(1)$,$\textrm{Q}(3)$ の距離 $\textrm{PQ}$ は
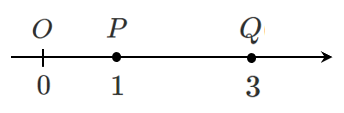
$\textrm{PQ}=3-1=2$
数直線上の2点間 $\textrm{P}(p)$,$\textrm{Q}(q)$ の距離は
$p<q$ のとき $q-p$ で求まる
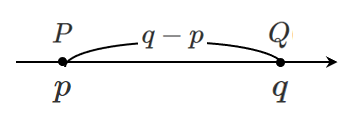
座標の大小関係を比べたときに 「大ー小」 で距離が求まる
数直線における内分点の座標
$a<b$ のとき
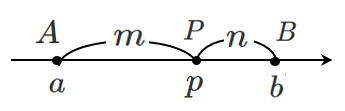
$a<p<b$ であるので,
$\textrm{AP}=p-a$,$\textrm{BP}=b-p$ である
$\textrm{AP}:\textrm{PB}=m:n$ より
$(p-a):(b-p)=m:n$
$n(p-a)=m(b-p)$
$np-na=mb-mp$
$mp+np=na+mb$
$(m+n)p=na+mb$
$\displaystyle{p=\frac{na+mb}{m+n}}$
$a>b$ のとき
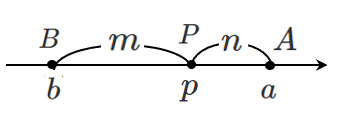
$b<p<a$ であるので,
$\textrm{AP}=a-p$,$\textrm{BP}=p-b$ である
$\textrm{AP}:\textrm{PB}=m:n$ より
$(a-p):(p-b)=m:n$
$n(a-p)=m(p-b)$
整理すると $\displaystyle{p=\frac{na+mb}{m+n}}$
2点 $\textrm{A}(a)$,$\textrm{B}(b)$ に対して,線分 $\textrm{AB}$ を $m:n$ に内分する点 $\textrm{P}$ の座標 $p$ は
$\displaystyle{p=\frac{na+mb}{m+n}}$

内分点の座標の覚え方はこれ!
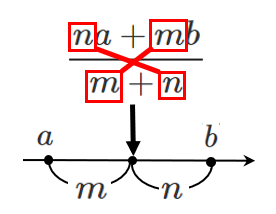

内分点の座標は「足してクロスにかける」と覚えよう!
数直線上における外分点の座標
$m>n$,$a<b$ のとき
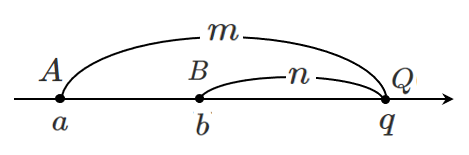
a<b<q$ より
$\textrm{AQ}=q-a$,$\textrm{BQ}=q-b$ である
$\textrm{AQ}:\textrm{QB}=m:n$ より
$(q-a):(q-b)=m:n$
$n(q-a)=m(q-b)$
$nq-na=mq-mb$
$mq-nq=-na+mb$
$(m-n)q=-na+mb$
$\displaystyle{q=\frac{-na+mb}{m-n}}$
$m>n$,$a<b$ のとき
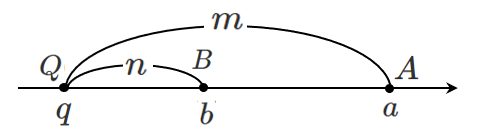
q<b<a$ より
$\textrm{AQ}=a-q$,$\textrm{BQ}=b-q$ である
$\textrm{AQ}:\textrm{QB}=m:n$ より
$(a-q):(b-q)=m:n$
$n(a-q)=m(b-q)$
整理すると $\displaystyle{q=\frac{-na+mb}{m-n}}$
2点 $\textrm{A}(a)$,$\textrm{B}(b)$ に対して,線分 $\textrm{AB}$ を $m:n$ に外分する点 $\textrm{Q}$ の座標 $q$ は
$\displaystyle{q=\frac{-na+mb}{m-n}}$

外分点の座標の覚え方はこれ!
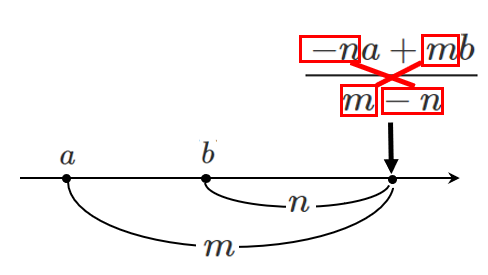

外分点の座標は「引いてクロスにかける」と覚えよう!
平面上の内分点・外分点の座標
$\textrm{P}(x,y)$ とすると
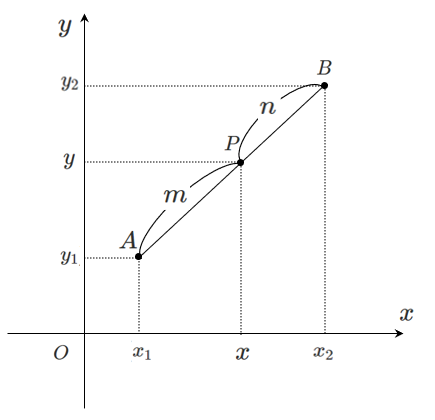
下図のように,点をとると
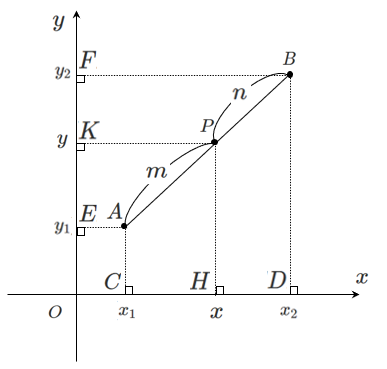
平行線と線分の比の関係より
$\textrm{CH}:\textrm{HD}=m:n$
$\textrm{EK}:\textrm{KF}=m:n$
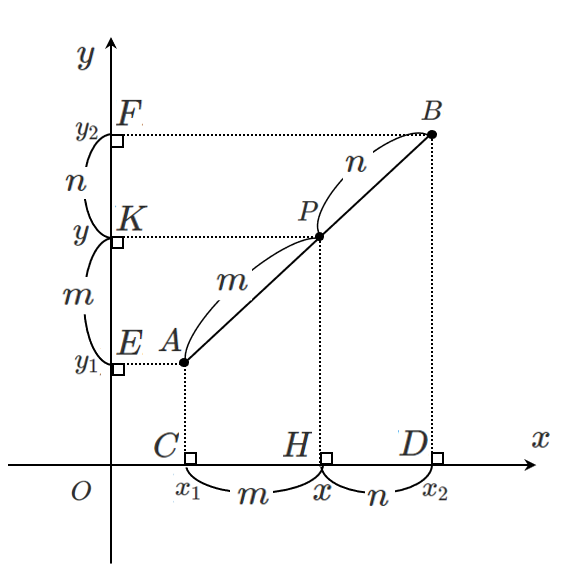
点 $\textrm{P}$ の $x$ 座標について
$\displaystyle{x=\frac{nx_1+mx_2}{m+n}}$
点 $\textrm{P}$ の $y$ 座標について
$\displaystyle{y=\frac{ny_1+my_2}{m+n}}$
したがって,点 $\textrm{P}$ の座標は
$\displaystyle{\left(\frac{nx_1+mx_2}{m+n},\frac{ny_1+my_2}{m+n}\right)}$

座標平面上では,$x$ 座標は $x$ 座標,$y$ 座標は $y$ 座標でそれぞれ求めればいいね!

外分点の座標も同様にして,求めることができるよ!
2点 $\textrm{A}(x_1,y_1)$,$\textrm{B}(x_2,y_2)$ を結ぶ線分 $\textrm{AB}$ を
$m:n$ に内分する点は $\displaystyle{\left(\frac{nx_1+mx_2}{m+n},\frac{ny_1+my_2}{m+n}\right)}$
$m:n$ に外分する点は $\displaystyle{\left(\frac{-nx_1+mx_2}{m-n},\frac{-ny_1+my_2}{m-n}\right)}$

式はややこしいけど,数直線上の内分点・外分点の公式を,$x$ 座標は $x$ 座標,$y$ 座標は $y$ 座標で使っているだけ!
使いながら覚えていこう!
中点の座標
中点とは,$1:1$ に内分することなので,
内分点の座標の公式を用いると
2点 $\textrm{A}(x_1,y_1)$,$\textrm{B}(x_2,y_2)$ を結ぶ線分 $\textrm{AB}$ の中点の座標は
$\displaystyle{\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)}$

中点の座標は使う場面が多いので,この公式を覚えておこう!
内分点・外分点の座標の公式を使う
(1) $3:2$ に内分する点
(2) $3:2$ に外分する点
(3) 中点
(1) $3:2$ に内分する点
$\displaystyle{\left(\frac{2\cdot(-1)+3\cdot4}{3+2},\frac{2\cdot2+3\cdot(-3)}{3+2}\right)}$ より
$\displaystyle{\left(2,-1\right)}$
(2) $3:2$ に外分する点
$\displaystyle{\left(\frac{-2\cdot(-1)+3\cdot4}{3-2},\frac{-2\cdot2+3\cdot(-3)}{3-2}\right)}$ より
$(14,-13)$
(3) 中点
$\displaystyle{\left(\frac{-1+4}{2},\frac{2-3}{2}\right)}$ より
$\displaystyle{\left(\frac{3}{2},-\frac{1}{2}\right)}$

図を描くことなく,内分点と外分点の座標が求まる公式だから便利だね!
まとめ
● 内分点・外分点の座標
2点 $\textrm{A}(x_1,y_1)$,$\textrm{B}(x_2,y_2)$ を結ぶ線分 $\textrm{AB}$ を
$m:n$ に内分する点は $\displaystyle{\left(\frac{nx_1+mx_2}{m+n},\frac{ny_1+my_2}{m+n}\right)}$
$m:n$ に外分する点は $\displaystyle{\left(\frac{-nx_1+mx_2}{m-n},\frac{-ny_1+my_2}{m-n}\right)}$
● 中点の座標
2点 $\textrm{A}(x_1,y_1)$,$\textrm{B}(x_2,y_2)$ を結ぶ線分 $\textrm{AB}$ の中点の座標は $\displaystyle{\left(\frac{x_1+x_2}{2},\frac{y_1+y_2}{2}\right)}$

忘れやすい公式なので,定期的に復習しよう!




コメント