高校数学Ⅱで学ぶ『円の方程式』について解説!
「中心と半径が求まれば円の方程式が求まる」ということを学び、
円の方程式に関する基礎を固めましょう!
この投稿を見れば、『円の方程式』はバッチリ!
図形と方程式

座標平面上の図形と方程式の関係をみてみよう!
方程式 … 文字が含まれる等式
例えば,$y=x$,$y=x^2$ など
方程式を満たす $x$ と $y$ の組合せを座標平面上にとると図形ができる
$y=x$ を満たすような $x$ と $y$ の組合せを座標で表すと
$(0,0)$,$(1,1)$,$(2,2)$,$(-1,-1)$,$\cdots$
$x$ 座標と $y$ 座標が等しいような点が $y=x$ を満たすような点である
これらを図示すると,座標平面上に直線ができる
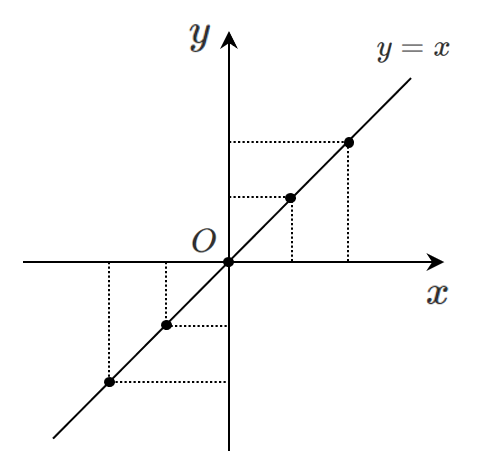
以上より,方程式 $y=x$ は座標平面上では直線を表す
円の方程式
円上の点 $\textrm{P}(x,y)$ とすると

点 $\textrm{P}$ が円周上のどこにあっても
$\textrm{CP}=r$ となる
$\textrm{CP}$ は点と点の距離なので
$\textrm{CP}=\sqrt{(x-a)^2+(y-b)^2}$
$\textrm{CP}=r$ より
$\sqrt{(x-a)^2+(y-b)^2}=r$
両辺を2乗して
$(x-a)^2+(y-b)^2=r^2$
点 $(a,b)$ を中心とする半径 $r$ の円の方程式は
$(x-a)^2+(y-b)^2=r^2$

$y^2$ が今までにない形だけど,円の方程式に慣れよう!
(1) 中心 $(1,-2)$,半径 $3$ の円
(2) 原点が中心,半径 $\sqrt{2}$ の円
(1) 中心 $(1,-2)$,半径$3$ の円
$(x-1)^2+\{y-(-2)\}^2=3^2$
すなわち $(x-1)^2+(y+2)^2=9$
(2) 原点が中心,半径 $\sqrt{2}$ の円
$x^2+y^2=(\sqrt{2})^2$
すなわち $x^2+y^2=2$

中心と半径が与えられたら,円の方程式が求まる!
円の方程式の決定

与えられた条件をもとに,円の中心と半径を求めよう!
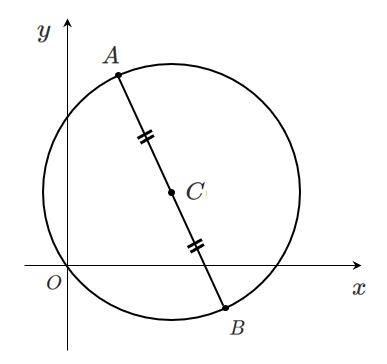
中心は線分 $\textrm{AB}$ の中点なので
$\displaystyle{\left(\frac{1+3}{2},\frac{3+(-1)}{2}\right)}$
すなわち $(2,1)$
中心を点 $\textrm{C}$ とすると
半径は点 $\textrm{A}(1,3)$ と点 $\textrm{C}(2,1)$ の距離なので
$\sqrt{(2-1)^2+(1-3)^2}=\sqrt{5}$
したがって,求める円の方程式は
$(x-2)^2+(y-1)^2=(\sqrt{5})^2$
すなわち $(x-2)^2+(y-1)^2=5$

中点の座標の求め方や点と点の距離の求め方はきちんとおさえておこう!
まとめ
● 円の方程式
点 $(a,b)$ を中心とする半径 $r$ の円の方程式は
$(x-a)^2+(y-b)^2=r^2$
中心と半径が求まれば,円の方程式も求まる

最初は難しく感じる式なので,問題を解きながら慣れることが大切!




コメント