
三角関数の $\sin\theta$ と $\cos\theta$ の値を学ぼう!
数学Ⅰの「三角比」の復習にもなるよ!
数学Ⅰの三角比の定義

まずは,数学Ⅰの「三角比」の復習から!
鋭角の三角比
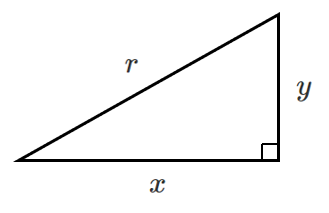
直角三角形の鋭角(90$^\circ$ 未満の角)の1つを $\theta$ とし,斜辺の長さを $r$ ,その他の辺の長さを下図のように $x$,$y$ とするとき,三角比の定義は以下のようになる。
● $\sin\theta$ の覚え方
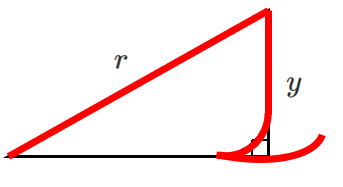
$s$ の筆記体で $\displaystyle{\sin\theta=\frac{y}{r}}$
● $\cos\theta$ の覚え方
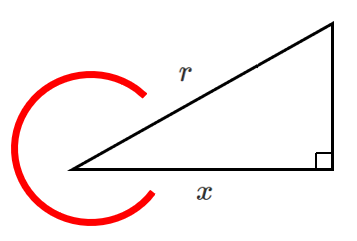
$c$ と書いて $\displaystyle{\cos\theta=\frac{x}{r}}$
● $\tan\theta$ の覚え方
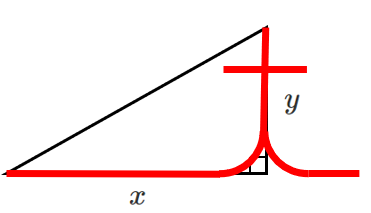
$t$ の筆記体で $\displaystyle{\tan\theta=\frac{y}{x}}$
鈍角の三角比

直角三角形では,鋭角しか三角比が定義できないので,
鈍角の三角比は座標で定義するよ!
座標平面上において原点を中心とする半径 $r$ の半円をかき,この半円と $x$ 軸の正の部分との交点を $A$ とする。
$∠AOP=\theta$ となる点 $P$ をこの半円上にとり,点 $P$ の座標を $(x,y)$ としたとき,
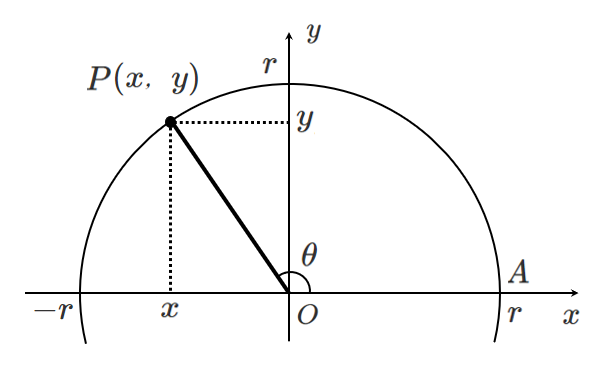

鋭角も鈍角も三角比の定義式は同じだね!

同じだけど,鈍角の $x$ と $y$ については座標になっていることに気を付けよう!
数学Ⅰ「三角比の値」の復習はこれ↓

三角関数の定義
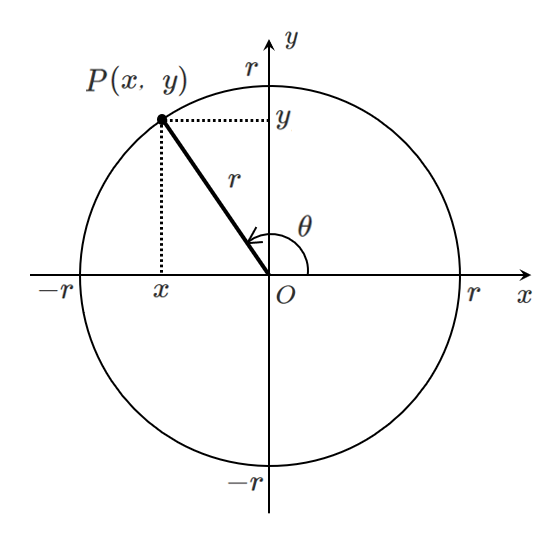
座標平面上において原点を中心とする半径 $r$ の円をかき,
下図のように点 $P(x,y)$ ,角 $\theta$ をとる
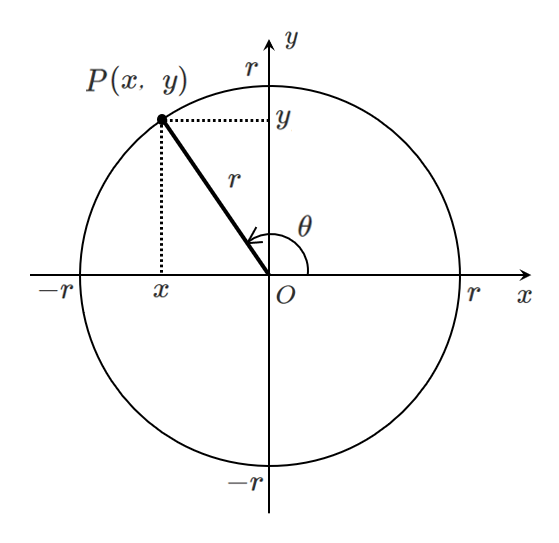

三角関数では,$180^\circ$ より大きい角も考える!
単位円を用いた三角関数の定義

$r=1$ の円(単位円)を考えると,$\sin\theta$ と $\cos\theta$ の定義がシンプルになるよ!
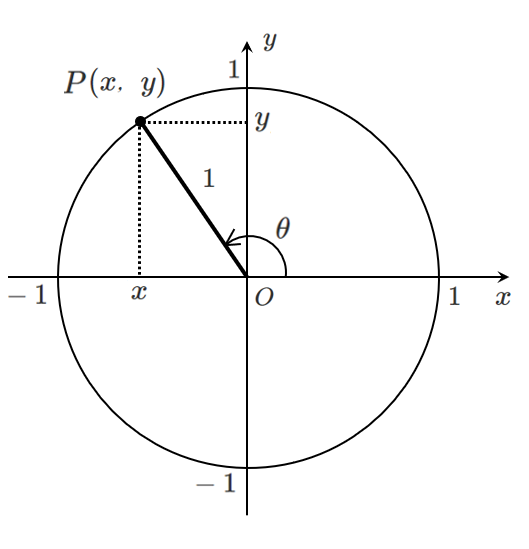
$$\sin\theta=\frac{y}{r},\cos\theta=\frac{x}{r}$$
$$ \Downarrow r=1とする$$
$$\sin\theta=y,\cos\theta=x$$
$\theta=\frac{\pi}{6},\frac{\pi}{4},\frac{\pi}{3}$ の sin と cos
用いる直角三角形

ここからは弧度法で考えよう!
$\displaystyle{\frac{\pi}{6}}$,$\displaystyle{\frac{\pi}{4}}$,$\displaystyle{\frac{\pi}{3}}$ の直角三角形の斜辺の長さを $1$ にする
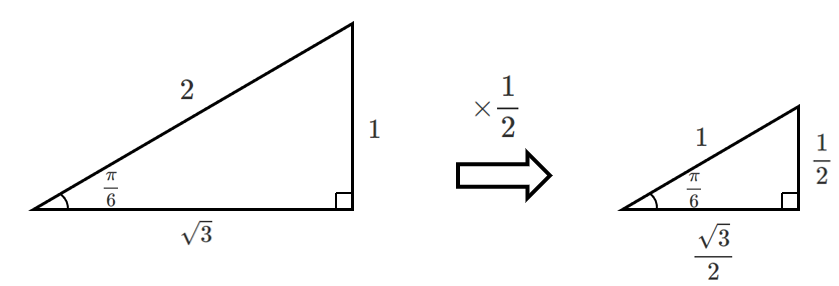
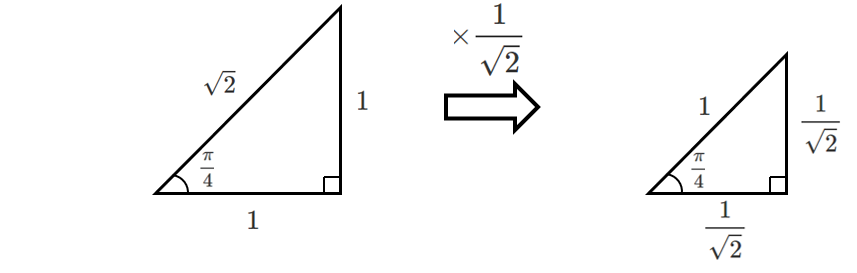
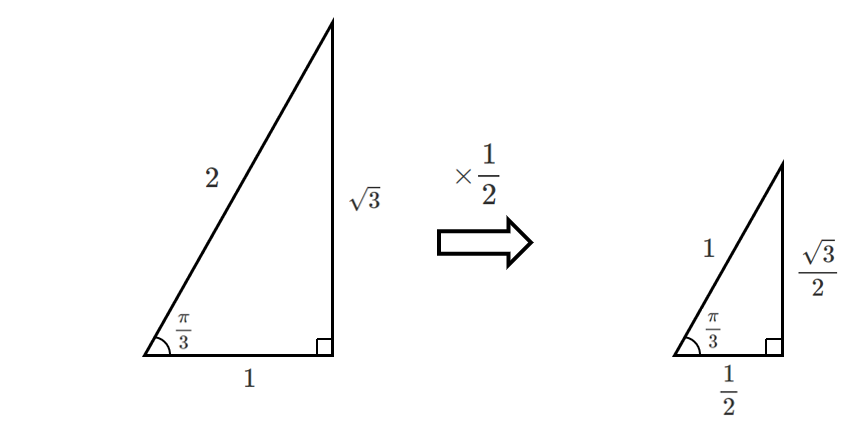

斜辺の長さを $1$ した直角三角形を作っておくと,単位円のときに考えやすい!
$\theta=\frac{\pi}{6}$
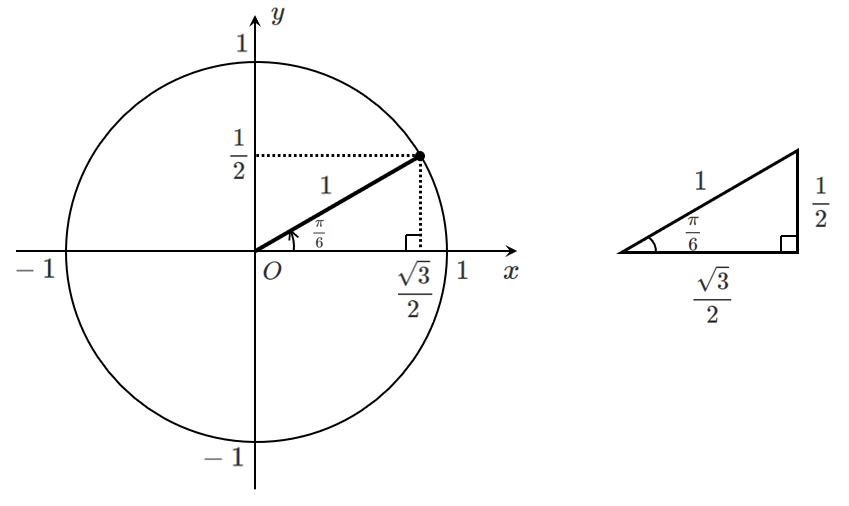
$$\displaystyle{\sin\frac{\pi}{6}=\frac{1}{2},\cos\frac{\pi}{6}=\frac{\sqrt{3}}{2}}$$
$\theta=\frac{\pi}{4}$
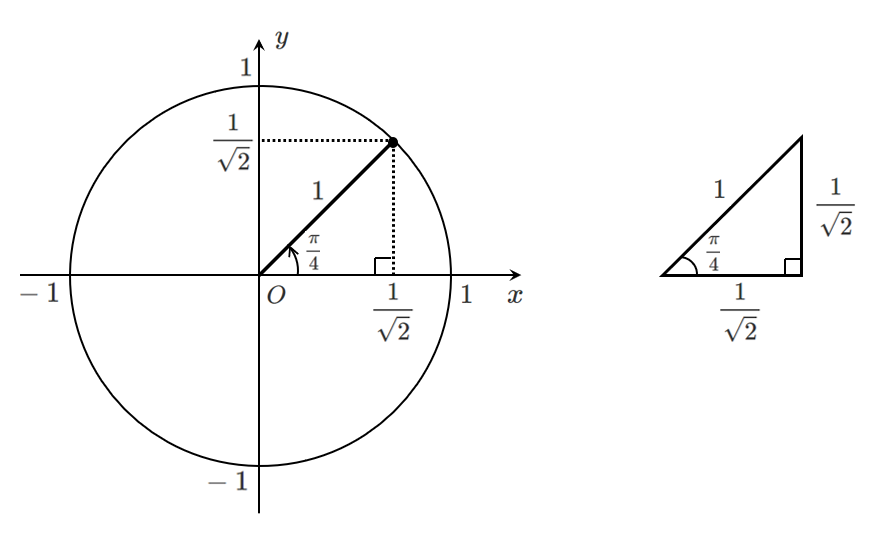
$$\displaystyle{\sin\frac{\pi}{4}=\frac{1}{\sqrt{2}},\cos\frac{\pi}{4}=\frac{1}{\sqrt{2}}}$$
$\theta=\frac{\pi}{3}$
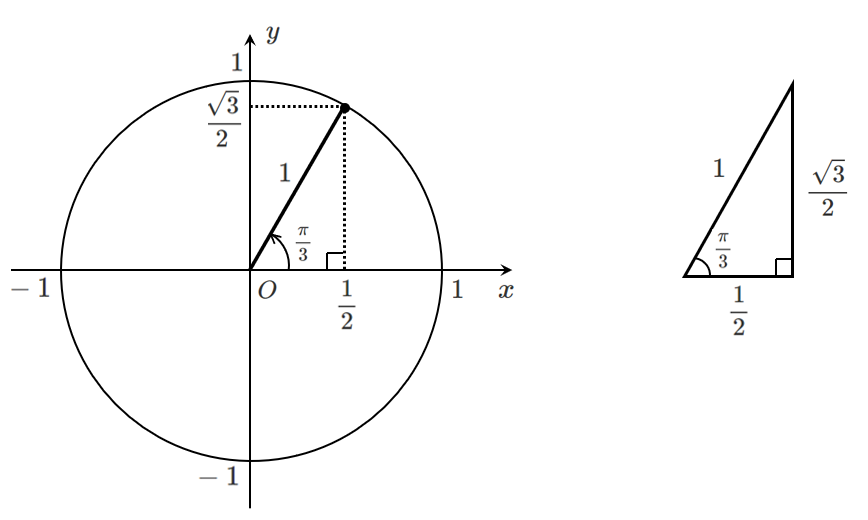
$$\displaystyle{\sin\frac{\pi}{3}=\frac{\sqrt{3}}{2},\cos\frac{\pi}{3}=\frac{1}{2}}$$
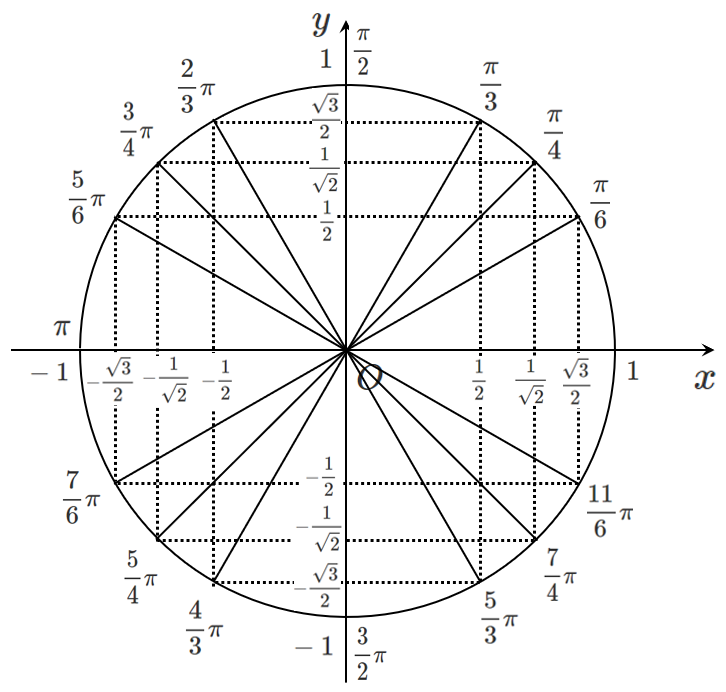
単位円周上の座標
$\displaystyle{\theta=\frac{\pi}{6},\frac{\pi}{4},\frac{\pi}{3}}$ のときの円周上の点から,
$x$ 軸,$y$ 軸に関して対称な点をとると以下のような図になる
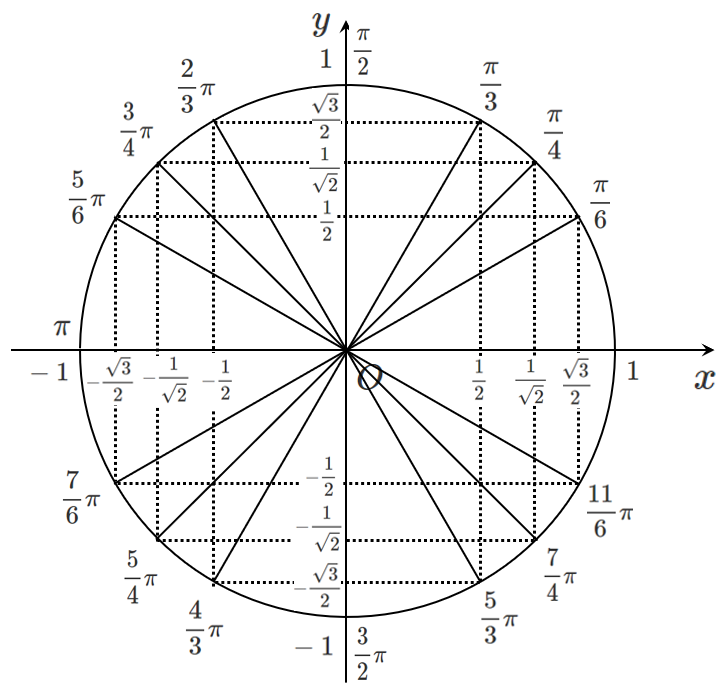

この図をもとに,sin と cos の値をまとめてみよう!
$\sin\theta$,$\cos\theta$ の値
| $\theta$ | $0$ | $\displaystyle{\frac{\pi}{6}}$ | $\displaystyle{\frac{\pi}{4}}$ | $\displaystyle{\frac{\pi}{3}}$ | $\displaystyle{\frac{\pi}{2}}$ | $\displaystyle{\frac{2}{3}\pi}$ | $\displaystyle{\frac{3}{4}\pi}$ | $\displaystyle{\frac{5}{6}\pi}$ | $\pi$ |
| $\sin\theta$ | $0$ | $\displaystyle{\frac{1}{2}}$ | $\displaystyle{\frac{1}{\sqrt{2}}}$ | $\displaystyle{\frac{\sqrt{3}}{2}}$ | $1$ | $\displaystyle{\frac{\sqrt{3}}{2}}$ | $\displaystyle{\frac{1}{\sqrt{2}}}$ | $\displaystyle{\frac{1}{2}}$ | $0$ |
| $\cos\theta$ | $1$ | $\displaystyle{\frac{\sqrt{3}}{2}}$ | $\displaystyle{\frac{1}{\sqrt{2}}}$ | $\displaystyle{\frac{1}{2}}$ | $0$ | $\displaystyle{-\frac{1}{2}}$ | $\displaystyle{-\frac{1}{\sqrt{2}}}$ | $\displaystyle{-\frac{\sqrt{3}}{2}}$ | $-1$ |
| $\theta$ | $\pi$ | $\displaystyle{\frac{7}{6}\pi}$ | $\displaystyle{\frac{5}{4}\pi}$ | $\displaystyle{\frac{4}{3}\pi}$ | $\displaystyle{\frac{3}{2}\pi}$ | $\displaystyle{\frac{5}{3}\pi}$ | $\displaystyle{\frac{7}{4}\pi}$ | $\displaystyle{\frac{11}{6}\pi}$ | $2\pi$ |
| $\sin\theta$ | $0$ | $\displaystyle{-\frac{1}{2}}$ | $\displaystyle{-\frac{1}{\sqrt{2}}}$ | $\displaystyle{-\frac{\sqrt{3}}{2}}$ | $-1$ | $\displaystyle{-\frac{\sqrt{3}}{2}}$ | $\displaystyle{-\frac{1}{\sqrt{2}}}$ | $\displaystyle{-\frac{1}{2}}$ | $0$ |
| $\cos\theta$ | $-1$ | $\displaystyle{-\frac{\sqrt{3}}{2}}$ | $\displaystyle{-\frac{1}{\sqrt{2}}}$ | $\displaystyle{-\frac{1}{2}}$ | $0$ | $\displaystyle{\frac{1}{2}}$ | $\displaystyle{\frac{1}{\sqrt{2}}}$ | $\displaystyle{\frac{\sqrt{3}}{2}}$ | $1$ |

特徴を整理するとこんな感じ!
- $\displaystyle{\theta=\frac{○}{4}\pi}$ のときは $\displaystyle{±\frac{1}{\sqrt{2}}$
- $\displaystyle{\theta=\frac{○}{6}\pi,\frac{○}{3}\pi}$ のときは $\displaystyle{±\frac{1}{2}}$ と $\displaystyle{±\frac{\sqrt{3}}{2}}$ の組合せ
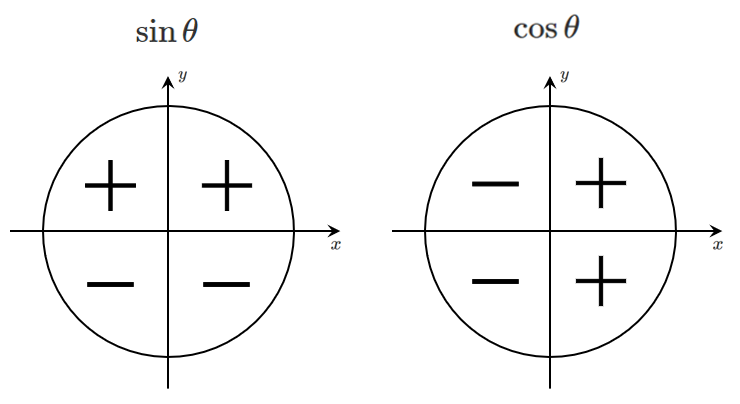
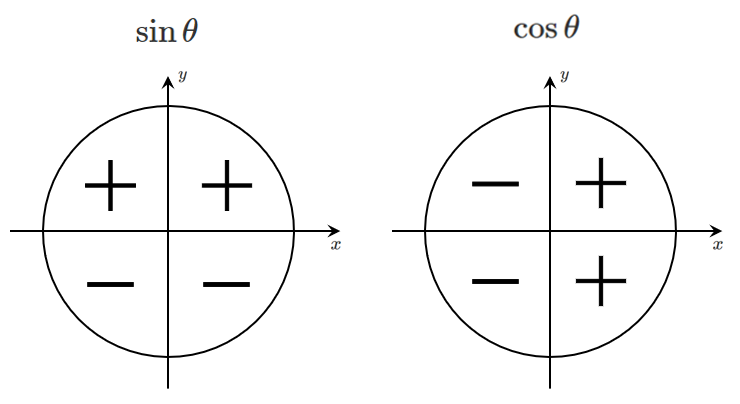
$\sin\theta$,$\cos\theta$ の符号

単位円において sin は $y$ 座標,cos は $x$ 座標ということを踏まえると,符号が決まるよ!
まとめ
● 三角関数の定義
$$\displaystyle{\sin\theta=\frac{y}{r},\cos\theta=\frac{x}{r},\tan\theta=\frac{y}{x}}$$
● 単位円を用いた sin と cos の定義
$r=1$ にすると $\sin\theta=y,\cos\theta=x$
$\sin\theta$ は単位円上の点の $y$ 座標,$\cos\theta$ は単位円上の点の $x$ 座標
● 単位円上の座標
● sin と cos の符号

sin と cos の値を確実に求められるようにしよう!




コメント