
三角関数を含む方程式の応用!
基本を復習してから学ぼう!
三角関数を含む方程式
$\sin$ は $y$ 座標
$\cos$ は $x$ 座標
$\sin$

「$\sin$ は $y$ 座標」を用いて方程式を解こう!
単位円における $y$ 座標が $\displaystyle{\frac{1}{2}}$ の点を求めると
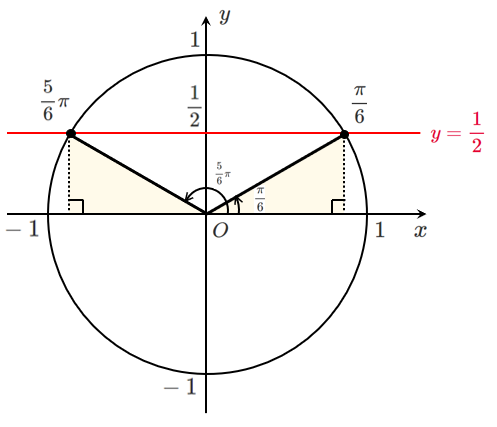
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{\pi}{6},\frac{5}{6}\pi}$

$0≦\theta<2\pi$ というのは,「1周で」という意味!

単位円で $\sin\theta$ の値を考えると下のような図になる!
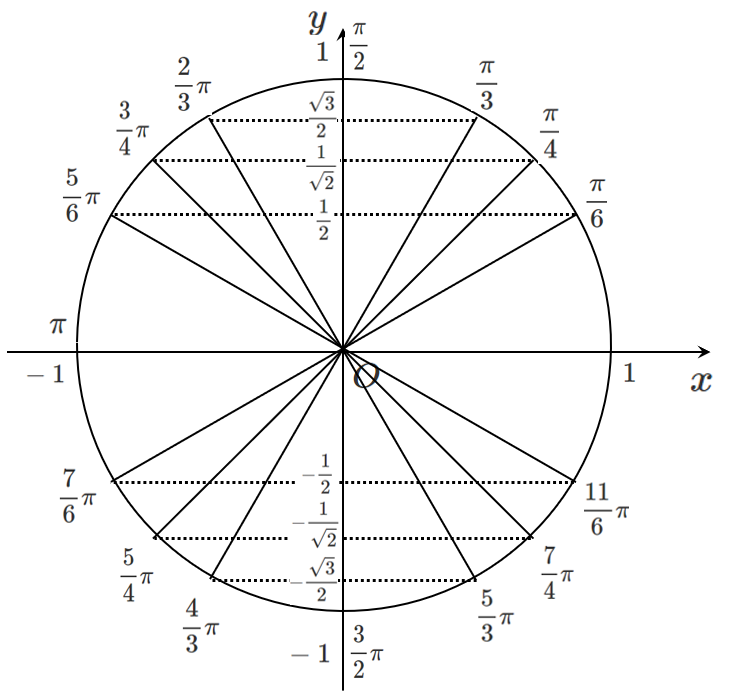
$\cos$

「$\cos$ は $x$ 座標」を用いて方程式を解こう!
単位円における $x$ 座標が $\displaystyle{-\frac{1}{2}}$ の点を求めると
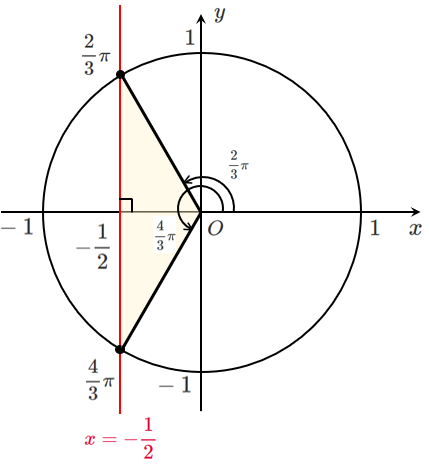
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{2}{3}\pi,\frac{4}{3}\pi}$

単位円で $\cos\theta$ の値を考えると下のような図になる!
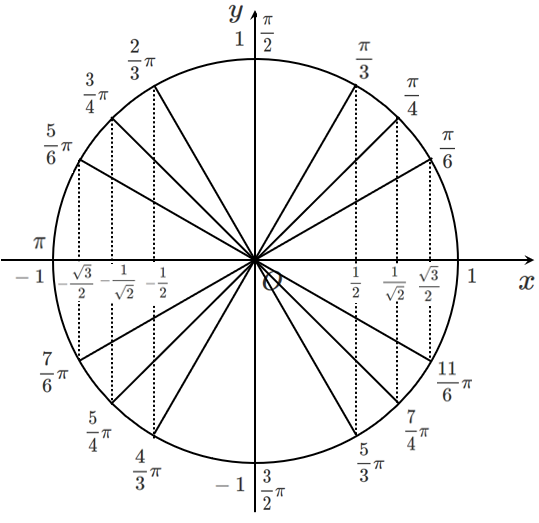

$\sin\theta$ も $\cos\theta$ も $\displaystyle{±\frac{1}{2},±\frac{1}{\sqrt{2}},±\frac{\sqrt{3}}{2}}$ のところに線を引くことになるね!

$\displaystyle{\frac{1}{2}<\frac{1}{\sqrt{2}}<\frac{\sqrt{3}}{2}}$ という大小関係を意識して線を引けば,角度は求まる!
詳しくはこれ↓
三角関数を含む方程式の応用

三角関数を含む方程式の応用問題を解いてみよう!
$\cos^2\theta=1-\sin^2\theta$ を用いて方程式を変形すると(三角関数の相互関係)
$2(1-\sin^2\theta)-3\sin\theta=0$
$-2\sin^2\theta-3\sin\theta+2=0$
$2\sin^2\theta+3\sin\theta-2=0$
$(2\sin\theta-1)(\sin\theta+2)=0$
$\displaystyle{\sin\theta=\frac{1}{2},-2}$
$0≦\theta<2\pi$ より,$-1≦\sin\theta≦1$ であるから
$\displaystyle{\sin\theta=\frac{1}{2}}$ ($\sin\theta≠-2$)
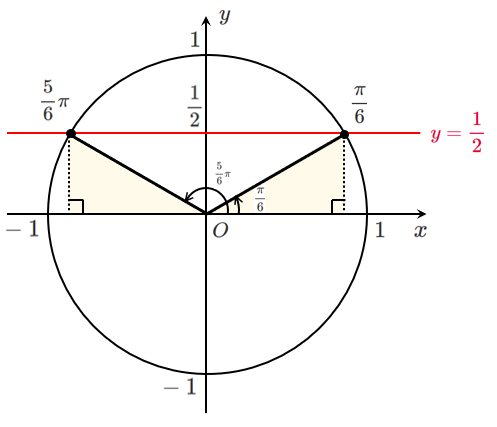
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{\pi}{6},\frac{5}{6}\pi}$
$2\sin^2\theta+3\sin\theta-2=0$
$(2\sin\theta-1)(\sin\theta+2)=0$
この式変形(因数分解)ができない場合は,以下の手順を参考
$2\sin^2\theta+3\sin\theta-2=0$ を $\sin\theta=A$ と置き換える
$2A^2+3A-2=0$ としてから $(2A-1)(A+2)=0$ と因数分解する
$A$ を $\sin\theta$ に戻して $(2\sin\theta-1)(\sin\theta+2)=0$
$\sin^2\theta=1-\cos^2\theta$ を用いて方程式を変形すると(三角関数の相互関係)
$2(1-\cos^2\theta)-3\cos\theta-3=0$
$-2\cos^2\theta-3\cos\theta-1=0$
$2\cos^2\theta+3\cos\theta+1=0$
$(2\cos\theta+1)(\cos\theta+1)=0$
$\displaystyle{\cos\theta=-\frac{1}{2},-1}$
$\displaystyle{\cos\theta=-\frac{1}{2}}$
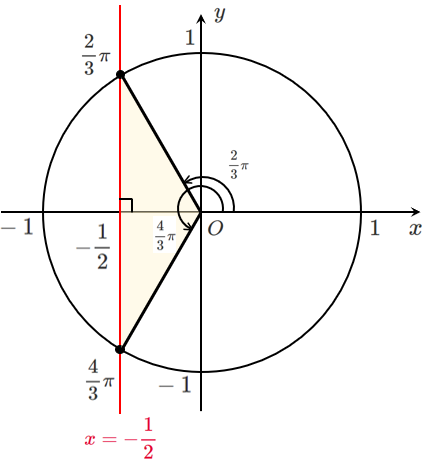
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{2}{3}\pi,\frac{4}{3}\pi}$
$\cos\theta=-1$
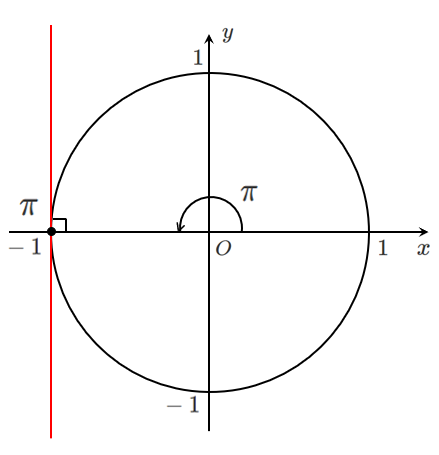
$0≦\theta<2\pi$ であるから $\theta=\pi$
以上より $\displaystyle{\theta=\frac{2}{3}\pi,\frac{4}{3}\pi,\pi}$

三角形の相互関係を使って,$\sin\theta$ または $\cos\theta$ だけにするところがポイントだね!

$-1≦\sin\theta≦1$,$-1≦\cos\theta≦1$ であることを踏まえて解くところもポイント!
まとめ
● 三角関数を含む方程式の応用問題のポイント
- $\sin^2\theta+\cos^2\theta=1$ を用いて,$\sin\theta$ だけ または $\cos\theta$ だけ の式にする
- $-1≦\sin\theta≦1$,$-1≦\cos\theta≦1$ を踏まえて解く
問題
$0≦\theta<2\pi$ のとき,次の方程式を解け。
(1) $2\cos^2\theta+3\sin\theta=0$
(2) $2\sin^2\theta+\sqrt{3}\sin\theta-2=0$
(1) $2\cos^2\theta+3\sin\theta=0$
$\cos^2\theta=1-\sin^2\theta$ を用いて方程式を変形すると
$2(1-\sin^2\theta)+3\sin\theta=0$
$-2\sin^2\theta+3\sin\theta+2=0$
$2\sin^2\theta-3\sin\theta-2=0$
$(2\sin\theta+1)(\sin\theta-2)=0$
$\displaystyle{\sin\theta=-\frac{1}{2},2}$
$0≦\theta<2\pi$ より,$-1≦\sin\theta≦1$ であるから
$\displaystyle{\sin\theta=-\frac{1}{2}}$ ($\sin\theta≠2$)
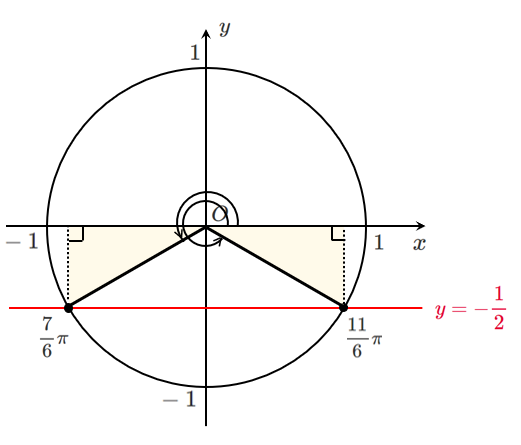
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{7}{6}\pi,\frac{11}{6}\pi}$
(2) $2\sin^2\theta+\sqrt{3}\sin\theta-2=0$
$\sin^2\theta=1-\cos^2\theta$ を用いて方程式を変形すると
$2(1-\cos^2\theta)+\sqrt{3}\cos\theta-2=0$
$-2\cos^2\theta+\sqrt{3}\cos\theta=0$
$2\cos^2\theta-\sqrt{3}\cos\theta=0$
$\cos\theta(2\cos\theta-\sqrt{3})=0$
$\displaystyle{\cos\theta=0,\frac{\sqrt{3}}{2}}$
$\cos\theta=0$
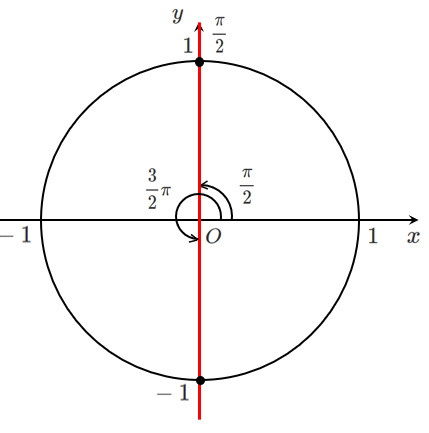
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{\pi}{2},\frac{3}{2}\pi}$
$\displaystyle{\cos\theta=\frac{\sqrt{3}}{2}}$
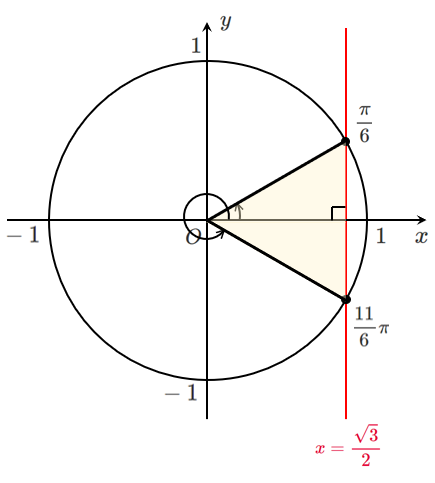
$0≦\theta<2\pi$ であるから $\displaystyle{\theta=\frac{\pi}{6},\frac{11}{6}\pi}$
以上より $\displaystyle{\theta=\frac{\pi}{2},\frac{3}{2}\pi,\frac{\pi}{6},\frac{11}{6}\pi}$

これが解けたら三角関数を含む方程式はばっちり!




コメント