
ベクトルの基本を学ぼう!
ベクトルとは
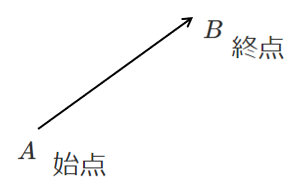
$A$ を始点,$B$ を終点とするとき,このベクトルを
$\overrightarrow{AB}$
と表す
ベクトルを $\vec{a}$,$\vec{b}$ などで表すこともある
$\vv{\textrm{AB}}$
ベクトルの大きさ
ベクトルは 大きさ と 向き を持つ量
向きは矢印の向きで表す
大きさは矢印の長さで表す
単に, $\overrightarrow{AB}$ とかくと大きさと向きが含まれている
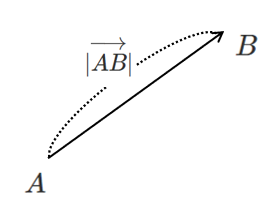
大きさのみを表したいときは絶対値記号を用いて
$|\overrightarrow{AB}|$
と表す
$|\vec{a}|$ は $\vec{a}$ の大きさ
$|\vec{b}|$ は $\vec{b}$ の大きさ
を表す
逆ベクトル
$\vec{a}$ と大きさが等しく,向きが反対のベクトルを
$\vec{a}$ の逆ベクトル
といい
$-\vec{a}$
で表す
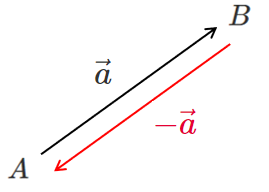
$\vec{a}=\overrightarrow{AB}$ のとき
$-\vec{a}=\overrightarrow{BA}$
すなわち
$\overrightarrow{BA}=-\overrightarrow{AB}$
等しいベクトル
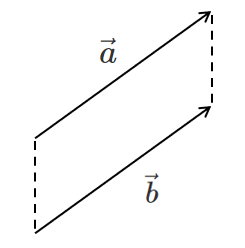
向きが同じで大きさも等しい2つのベクトル $\vec{a}$, $\vec{b}$ は等しい
といい
$\vec{a}=\vec{b}$
とかく
向きと大きさのどちらかが異なる場合は2つのベクトル $\vec{a}$, $\vec{b}$ は等しくない
向きは等しいが大きさが異なる
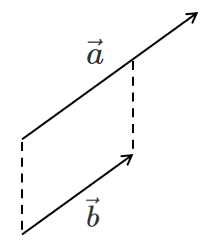
大きさは等しいが向きが異なる
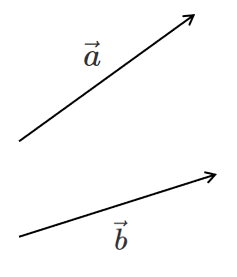
$\vec{a}≠\vec{b}$
$\vec{a}$ と $\vec{b}$ の大きさが等しい場合は
$|\vec{a}|=|\vec{b}|$
と表すことができる
ベクトルの加法

ベクトルの加法のルールを覚えよう!
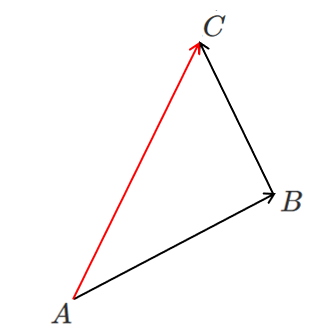
$\overrightarrow{AB}+ \overrightarrow{BC}= \overrightarrow{AC}$

始点と終点をくっつければ,簡単に和が求まるね!
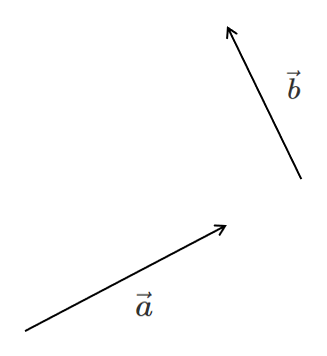
向きと大きさが等しければ,ベクトルは等しいので
$\vec{a}$ の終点に $\vec{b}$ の始点がくっつくように
$\vec{b}$ を平行移動すると
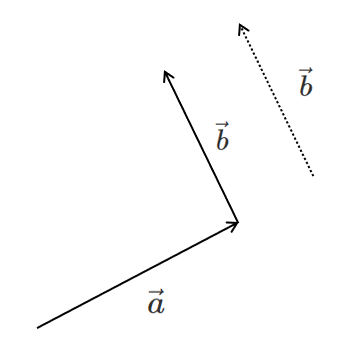
したがって, $\vec{a}+\vec{b}$ を図示すると
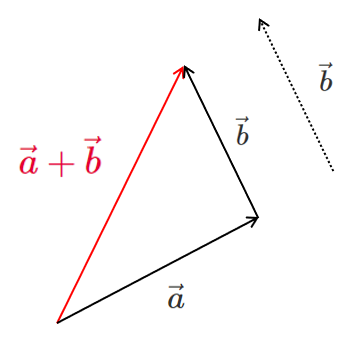

ベクトルの和は,
平行移動して始点と終点をくっつける!
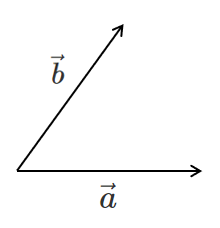
$\vec{a}+\vec{b}$ を図示すると
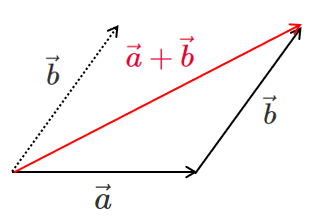
平行四辺形を使ったベクトルの和
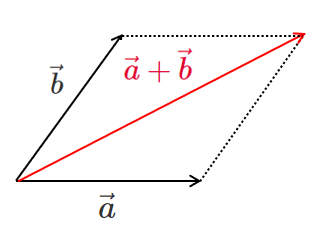

始点がくっついていたら,
平行四辺形の対角線が和になるね!

単に暗記するのではなく,ベクトルの和の基本を理解しておこう!
まとめ
● ベクトルとは
大きさと向きをもつ量 $\overrightarrow{AB}$ や $\vec{a}$ など
● ベクトルの大きさ
$\overrightarrow{AB}$ の大きさを $|\overrightarrow{AB}|$ と表す
● 等しいベクトル
$\vec{a}= \vec{b}$ とは $\vec{a}$ と $\vec{b}$ の大きさと向きがともに等しい

● ベクトルの加法

$\overrightarrow{AB}+ \overrightarrow{BC}= \overrightarrow{AC}$

何事も基本が大切!




コメント