ベクトルの減法

ベクトルの減法は加法から考えることが重要!
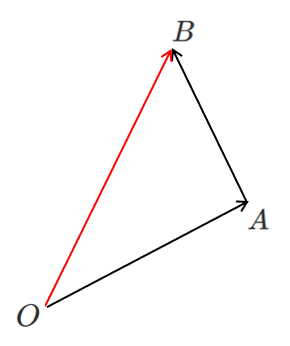
$\overrightarrow{OA}+ \overrightarrow{AB}= \overrightarrow{OB}$
この式を変形すると
$\overrightarrow{OB}- \overrightarrow{OA}= \overrightarrow{AB}$
という式が作れる
$\overrightarrow{OA}=\vec{a}$, $\overrightarrow{OB}=\vec{b}$ として, 図にしてみると
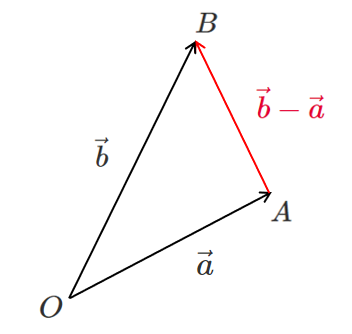
逆に
$\overrightarrow{AB}=\vec{b}-\vec{a}$
とすると
$\overrightarrow{BA}=-(\vec{b}-\vec{a})= \vec{a}-\vec{b} $
と表せるので
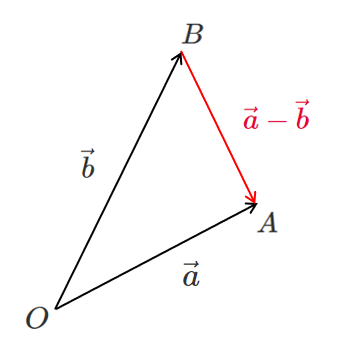

$\vec{a}-\vec{b}$ と $\vec{b}-\vec{a}$ のどっちがどっちか分からなくなりそう…

そうだよね!
ベクトルの減法は苦手な人が多いところだよ!
ポイントは「加法で考えること」!
$\overrightarrow{OA}-\overrightarrow{OB}$ は $\overrightarrow{AB}$ と $\overrightarrow{BA}$ のどっち?
加法に変形して式変形すると
\begin{eqnarray} \overrightarrow{OA}-\overrightarrow{OB} &=& \overrightarrow{OA}+(- \overrightarrow{OB}) \\ &=& \overrightarrow{OA}+ \overrightarrow{BO} \\ &=& \overrightarrow{BO}+ \overrightarrow{OA} \\ &=& \overrightarrow{BA} \\ \end{eqnarray}

加法にすることが大切だね!
$\vec{a}-\vec{b}$ の図示

加法を用いると $\vec{a}-\vec{b}$ の図示も簡単だよ!
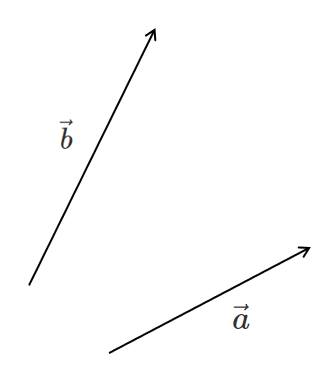
$\vec{a}-\vec{b}$ を式変形する
$\vec{a}-\vec{b}=\vec{a}+(-\vec{b})$
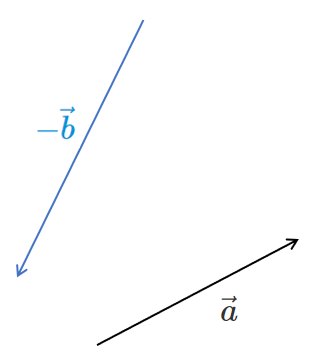
つまり,$\vec{a}$ と $-\vec{b}$ の和が $\vec{a}-\vec{b}$

ベクトルの差の分解

ベクトルの問題で使う場面が多い「差の分解」をマスターしよう!
ベクトルの「差の分解」とは
例えば
$\overrightarrow{AB}$ を $\overrightarrow{OB}- \overrightarrow{OA}$ に変形すること
$\overrightarrow{AB}= \overrightarrow{OB}- \overrightarrow{OA}$ になる理由は加法で説明できる
\begin{eqnarray} \overrightarrow{OB}-\overrightarrow{OA} &=& \overrightarrow{OB}-(- \overrightarrow{AO}) \\ &=& \overrightarrow{OB}+ \overrightarrow{AO} \\ &=& \overrightarrow{AO}+ \overrightarrow{OB} \\ &=& \overrightarrow{AB} \\ \end{eqnarray}同様に, $\overrightarrow{OC}- \overrightarrow{OD}$ を計算してみると
\begin{eqnarray} \overrightarrow{OC}-\overrightarrow{OD} &=& \overrightarrow{OC}-(- \overrightarrow{DO}) \\ &=& \overrightarrow{OC}+ \overrightarrow{DO} \\ &=& \overrightarrow{DO}+ \overrightarrow{OC} \\ &=& \overrightarrow{DC} \\ \end{eqnarray}以上より,
$\overrightarrow{AB}= \overrightarrow{OB}- \overrightarrow{OA}$
$\overrightarrow{DC}=\overrightarrow{OC}- \overrightarrow{OD}$
共通点を見ていると
$\overrightarrow{△□}=\overrightarrow{O□}- \overrightarrow{O△}$
となることが分かる
つまり
$\overrightarrow{BC}= \overrightarrow{OC}- \overrightarrow{OB}$
$\overrightarrow{FE}=\overrightarrow{OE}- \overrightarrow{OF}$

「後ー前」や「終点ー始点」で覚えよう!
右辺の始点は $O$ である必要があるか考えてみる
始点を $P$ にして $\overrightarrow{PB}- \overrightarrow{PA}$ を考えてみると
\begin{eqnarray} \overrightarrow{PB}-\overrightarrow{PA} &=& \overrightarrow{PB}-(- \overrightarrow{AP}) \\ &=& \overrightarrow{PB}+ \overrightarrow{AP} \\ &=& \overrightarrow{AP}+ \overrightarrow{PB} \\ &=& \overrightarrow{AB} \\ \end{eqnarray}$ \overrightarrow{AB}= \overrightarrow{PB}- \overrightarrow{PA}$ であることが分かる
以上より
$\overrightarrow{△□}=\overrightarrow{●□}- \overrightarrow{●△}$
と表せる
$\overrightarrow{AB}$ に差の分解を用いると
$ \overrightarrow{AB}= \overrightarrow{OB}- \overrightarrow{OA}$
$ \overrightarrow{AB}= \overrightarrow{PB}- \overrightarrow{PA}$
$ \overrightarrow{AB}= \overrightarrow{CB}- \overrightarrow{CA}$
$ \overrightarrow{AB}= \overrightarrow{GB}- \overrightarrow{GA}$
など
始点を自由に定めることができる

ベクトルの差の分解を用いると,始点も自由に決められる!
問題に合った始点を定めることが大切!
まとめ
● ベクトルの減法
$\overrightarrow{OB}- \overrightarrow{OA}= \overrightarrow{AB}$

● $\vec{a}-\vec{b}$ の図示
$\vec{a}+(-\vec{b})$ として考えることがポイント
● ベクトルの差の分解
$\overrightarrow{△□}=\overrightarrow{●□}- \overrightarrow{●△}$

ポイントをおさえれば,ベクトルの減法は簡単!




コメント