ベクトルの成分表示
ベクトルの向きや大きさを正確に表す方法として「ベクトルの成分表示」がある
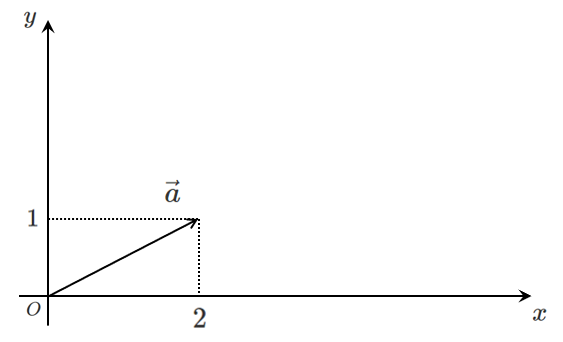
例えば,以下のベクトル $\vec{a}$ を成分表示してみよう
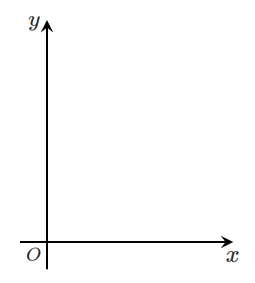
$x$ 軸,$y$ 軸をとる
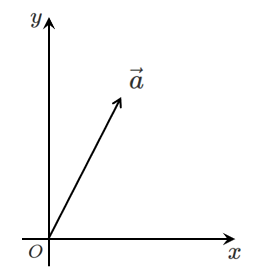
原点を始点にとる
終点の座標は $(1,2)$
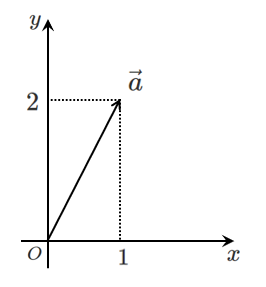
このとき,$\vec{a}=(1,2)$ と表す
まとめると
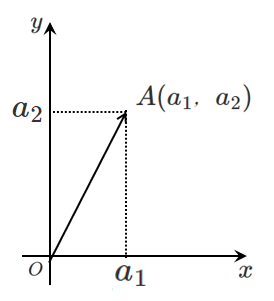
$A(a_1,a_2)$ のとき, $\overrightarrow{OA}=(a_1,a_2)$
$a_1$ を $x$ 成分,$a_2$ を $y$ 成分という
このように考えれば,平面上のどのようなベクトルも成分表示できる
成分表示におけるベクトルの大きさ
$\vec{a}=(1,2)$ の大きさ $|\vec{a}|$ を考える

$(1,2)$ を点 $A$ とすると
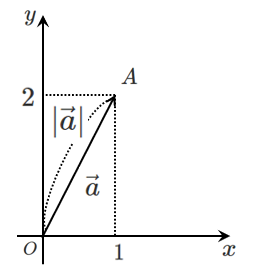
$|\vec{a}|$ は2点間の距離 $OA$ と等しいので
\begin{eqnarray} |\vec{a}| &=& OA \\ &=& \sqrt{1^2+2^2} \\ &=& \sqrt{5} \end{eqnarray}以上より,成分表示におけるベクトルの大きさは以下のようになる

「図形と方程式」で習った2点間の距離を使えばいいね!
成分表示の計算

成分表示の計算を考えてみよう!
$\vec{a}+\vec{b}$
$\vec{a}=(3,1)$,$\vec{b}=(2,1)$ のとき,$\vec{a}+\vec{b}$ を図で考える
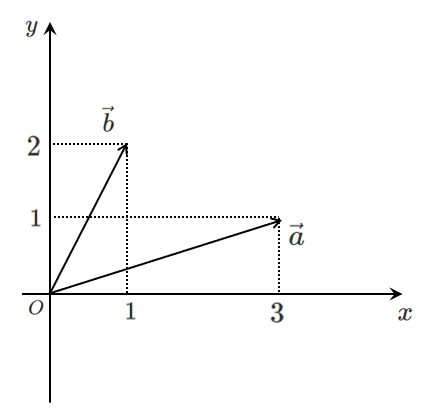
$\vec{b}$ を平行移動して,$\vec{a}+\vec{b}$ を求めると(ベクトルの加法)
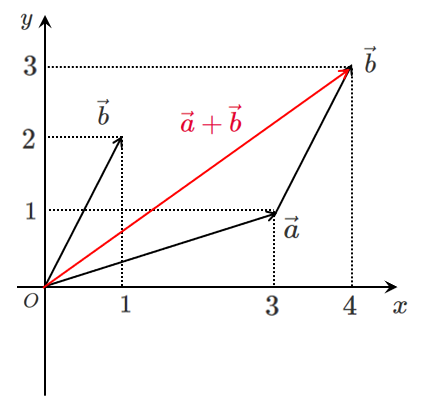
$\vec{a}+\vec{b}=(4,3)$
$x$ 成分の $4$ は $\vec{a}$ の $x$ 成分の $3$ と $\vec{b}$ の $x$ 成分の $1$ を足したもの
$y$ 成分の $3$ は $\vec{a}$ の $y$ 成分の $1$ と $\vec{b}$ の $y$ 成分の $2$ を足したもの
以上より,$\vec{a}+\vec{b}$ は以下のような計算ができる
\begin{eqnarray} \vec{a}+\vec{b} &=& (3,1)+(1,2) \\ &=& (3+1,1+2)\\ &=& (4,3) \end{eqnarray}$\vec{a}-\vec{b}$
$\vec{a}=(3,1)$,$\vec{b}=(2,1)$ のとき,$\vec{a}-\vec{b}$ を図で考える

$\vec{a}-\vec{b}$ を $\vec{a}+(-\vec{b})$ と考えると(ベクトルの減法)
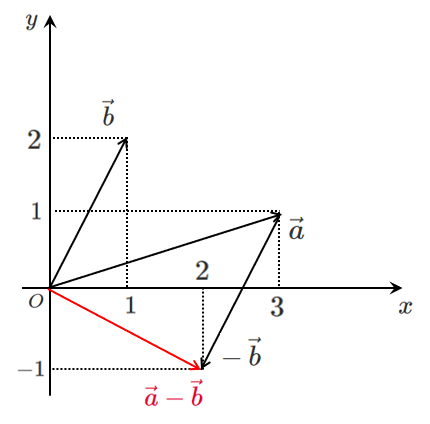
$\vec{a}-\vec{b}=(2,-1)$
$x$ 成分の $2$ は $\vec{a}$ の $x$ 成分の $3$ と $\vec{b}$ の $x$ 成分の $1$ を引いたもの
$y$ 成分の $-1$ は $\vec{a}$ の $y$ 成分の $1$ と $\vec{b}$ の $y$ 成分の $2$ を引いたもの
以上より,$\vec{a}-\vec{b}$ は以下のような計算ができる
\begin{eqnarray} \vec{a}-\vec{b} &=& (3,1)-(1,2) \\ &=& (3-1,1-2)\\ &=& (2,-1) \end{eqnarray}$k\vec{a}$
$\vec{a}=(2,1)$ のとき,$k\vec{a}$ ($k$ は実数)を図で考える
$2\vec{a}$ を図示すると
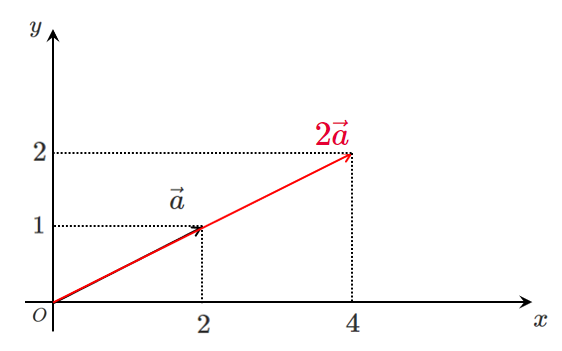
$2\vec{a}=(4,2)$
$\vec{a}$ の $x$ 成分と $y$ 成分をそれぞれ $2$ 倍したもの
以下のような計算ができる
\begin{eqnarray} 2\vec{a} &=& 2(2,1) \\ &=& (2\cdot2,2\cdot1)\\ &=& (4,2) \end{eqnarray}$-2\vec{a}$ を図示すると
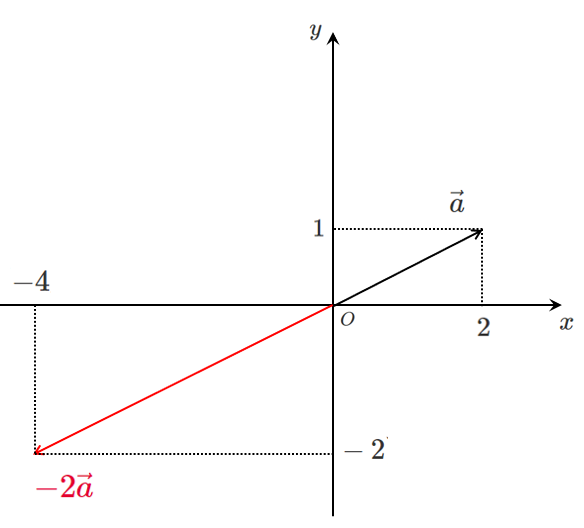
$-2\vec{a}=(-4,-2)$
$\vec{a}$ の $x$ 成分と $y$ 成分をそれぞれ $-2$ 倍したもの
以下のような計算ができる
\begin{eqnarray} -2\vec{a} &=& -2(2,1) \\ &=& (-2\cdot2,-2\cdot1)\\ &=& (-4,-2) \end{eqnarray}以上をまとめると
1 $(a_1,a_2)+(b_1,b_2)=(a_1+b_1,a_2+b_2)$
2 $(a_1,a_2)-(b_1,b_2)=(a_1-b_1,a_2-b_2)$
3 $k(a_1,a_2)=(ka_1,ka_2)$
原点以外が始点のベクトル
座標平面上にある2点 $A(3,1)$,$B(1,2)$ がある
$\overrightarrow{AB}$ を成分表示しよう
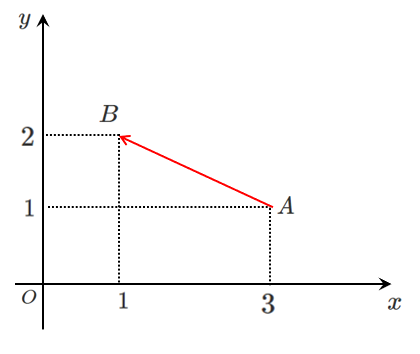
$\overrightarrow{OA}=(3,1)$,$\overrightarrow{OB}=(1,2)$
$\overrightarrow{AB}= \overrightarrow{OB}- \overrightarrow{OA}$ より(ベクトルの減法)
\begin{eqnarray} \overrightarrow{AB} &=& \overrightarrow{OB}- \overrightarrow{OA} \\ &=& (1,2)-(3,1)\\ &=& (-2,1) \end{eqnarray}

始点が原点ではないベクトルも「ベクトルの減法」を用いれば,成分表示できるね!
まとめ
● ベクトルの成分表示
$A(a_1,a_2)$ について,$\overrightarrow{OA}=(a_1,a_2)$
● 成分表示におけるベクトルの大きさ
$\vec{a}=(a_1,a_2)$ のとき $|\vec{a}|=\sqrt{a_1^2+a_2^2}$
● 成分表示の計算
1 $(a_1,a_2)+(b_1,b_2)=(a_1+b_1,a_2+b_2)$
2 $(a_1,a_2)-(b_1,b_2)=(a_1-b_1,a_2-b_2)$
3 $k(a_1,a_2)=(ka_1,ka_2)$

これで成分表示の基本はばっちり!




コメント