
ベクトルの内積の基本をおさえよう!
ベクトルの内積
$\vec{a}$ と $\vec{b}$ のなす角を $\theta$ とすると
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$
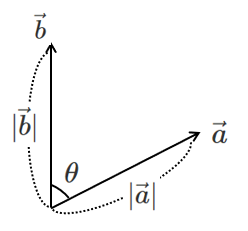
なす角は「始点を合わせたときの角度」のこと
<注意>
$\vec{a}\cdot\vec{b}$ と $\vec{a}×\vec{b}$ は同じではない
$\vec{a}×\vec{b}$ はベクトルの外積という(大学で習う)

「大きさ×大きさ×cosなす角」と覚えておこう!

内積って結局何なの?

それじゃあ内積の意味を学んでみよう!
内積の数学的意味
$\triangle OAB$ において,$\overrightarrow{OA}=\vec{a}$, $\overrightarrow{OB}=\vec{b}$ とする
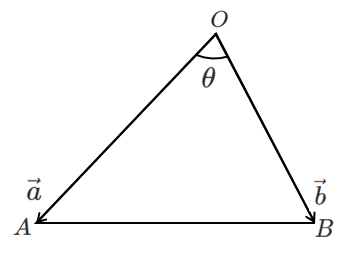
余弦定理を用いると,
$BA^2=OA^2+OB^2-2\cdot OA\cdot OB\cos\theta$
$\overrightarrow{BA}=\vec{a}-\vec{b}$ より(ベクトルの減法)
$|\vec{a}-\vec{b}|^2=|\vec{a}|^2+|\vec{b}|^2-2|\vec{a}||\vec{b}|\cos\theta$
$|\vec{a}-\vec{b}|^2$ の計算をする際に,
$|\vec{a}||\vec{b}|\cos\theta$
が式に必ず含まれる
数学の問題では $|\vec{a}-\vec{b}|^2$ などの計算をすることが多いので
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$
とすると
$|\vec{a}-\vec{b}|^2=|\vec{a}|^2+|\vec{b}|^2-2\vec{a}\cdot\vec{b}$
という形になり
$(a-b)^2=a^2-2ab+b^2$
の展開公式と似たような形になり,計算を考えやすくなる
内積の物理的意味

物理と数学は深い関係にある!
物理における内積の扱いを考えてみよう!

仕事って何だっけ?
ある物体を $F$ $[N]$ の力で,力の向きと同じ方向に $x$ $[m]$ 引っ張ったときの仕事 $W$ $[J]$ は
$W=F\cdot x$
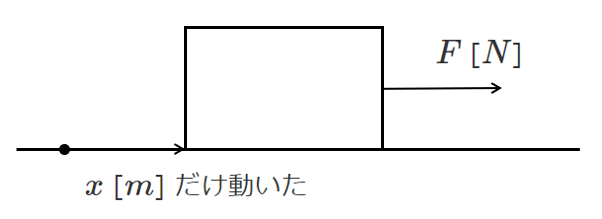
仕事 $W$ $[J]$ は $F\cdot x$ である
これをベクトルで表現すると
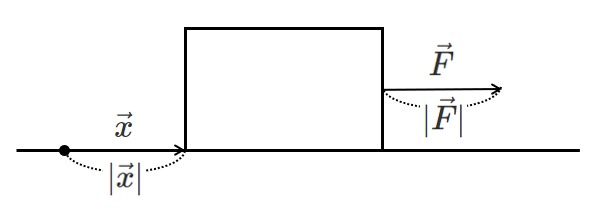
$W=|\vec{F}||\vec{x}|$
力の向きと移動する向きが異なっている場合は
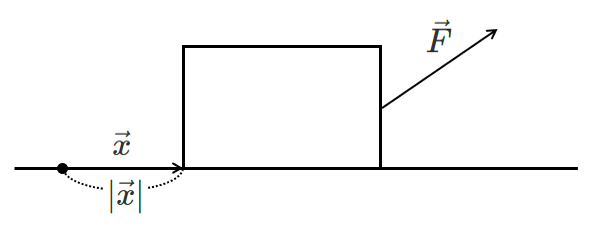
向きをそろえるために,$\vec{F}$ の水平方向の成分をつくる
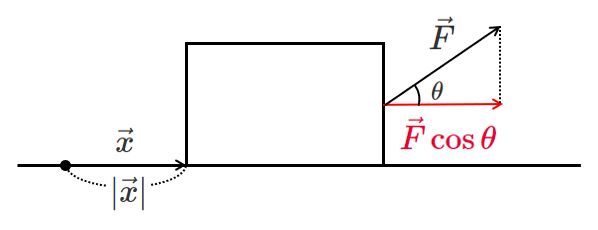
$\vec{F}$ の水平方向の成分は $\vec{F}\cos\theta$
よって, $\vec{F}$ の水平方向の成分の大きさは $|\vec{F}|\cos\theta$
したがって,仕事 $W$ $[J]$ は
$W=|\vec{F}||\vec{x}|\cos\theta$
$|\vec{F}||\vec{x}|\cos\theta$ は内積 $\vec{F}\cdot\vec{x}$ なので
$W=\vec{F}\cdot\vec{x}$

つまり,内積は「力のした仕事」を表しているね!

$cos\theta$ が出てくる理由は,移動した方向と力の向きをそろえるためだったんだね!
まとめ
● ベクトルの内積
$\vec{a}$ と $\vec{b}$ のなす角を $\theta$ とすると
$\vec{a}\cdot\vec{b}=|\vec{a}||\vec{b}|\cos\theta$

内積の意味を理解できたかな?




コメント